![Примеры уроков. ЕГЭ по математике (базовый уровень) для 10-11 классов [Примеры уроков. ЕГЭ по математике (базовый уровень) для 10-11 классов]](/img/theme/subjects/math-64.png) | Примеры уроков. ЕГЭ по математике (базовый уровень) для 10-11 классовПримеры уроков. ЕГЭ по математике (базовый уровень) для 10-11 классов |
Примеры уроков онлайн-курса по школьной программе
Примеры уроков онлайн-курса по школьной программе
1 урок
Арифметические вычисления
Порядок действий: первыми выполняются операции умножения и деления, затем - сложения и вычитания. Если нужно изменить порядок, то ставят скобки.
Пример. Вычислить $\displaystyle \frac {\Big(152 \frac{3}{4} - 148 \frac{3}{8} \Big) \cdot 0{,}3} {0{,}2}$.
Решение. $\displaystyle 1) \ 152 \frac{3}{4} - 148 \frac{3}{8}=4\frac{3}{8}=4{,}375$.
$\displaystyle 2)\ 4{,}375 \cdot 0{,}3=1{,}3125$.
$\displaystyle 3)\ 1{,}3125:0{,}2=6{,}5625$.
Ответ: $\displaystyle 6{,}5625$.
Степень
Свойства степени при $\displaystyle a>0, \ b>0$:
$\displaystyle a^{-n}=\frac{1}{a^n}$
$\displaystyle a^n \cdot a^m=a^{n+m}$
$\displaystyle \frac{a^n}{a^m}=a^{n-m}$
$\displaystyle \Big(a^n \Big)^m=a^{nm}$
$\displaystyle (ab)^n=a^n \cdot b^n$
$\displaystyle \Big(\frac{a}{b} \Big)^n= \frac{a^n}{b^n}$
Пример. $\displaystyle \frac{5^6 \cdot 125}{25^4}$.
Решение.$\displaystyle \frac{5^6 \cdot 125}{25^4}=\frac{5^6\cdot 5^3}{(5^2)^4}=\frac{5^9}{5^8}=5.$
Ответ:$\displaystyle 5$.
Модуль числа
Модуль числа (абсолютная величина числа):
\begin{equation*} \lvert a\rvert= \begin{cases} \displaystyle a, если \ a\geqslant0\\ \displaystyle -a, если \ a<0\end{cases} \end{equation*}
Пример. Упростите: $\displaystyle \lvert -3 \rvert + \lvert 5-2 \rvert - \lvert -3-6 \rvert + \lvert 1-4 \rvert$.
Решение. $\displaystyle \lvert -3 \rvert + \lvert 5-2 \rvert - \lvert -3-6 \rvert + \lvert 1-4 \rvert=3+3-9+3=0$.
Ответ: $\displaystyle 0$.
Геометрический смысл модуля: $\displaystyle \lvert a \rvert$ - это расстояние от числа $\displaystyle a$ до нуля на числовой прямой.
Пример. На координатной прямой отмечены числа $\displaystyle -0{,}205; \ -0{,}052; \ 0{,}02; \ 0{,}008$. Какое из этих чисел удалено от нуля на наибольшее расстояние?
Решение.$\displaystyle \lvert -0{,}205 \rvert=0{,}205; \ \lvert -0{,}052 \rvert=0{,}052; \ \lvert 0{,}02 \rvert=0{,}02; \ \lvert 0{,}008 \rvert=0{,}008$.
Сравнение модулей показывает, что $\displaystyle 0{,}205$ больше остальных, значит, число $\displaystyle -0{,}205$ удалено от нуля на наибольшее расстояние (см. рисунок)
Ответ:$\displaystyle -0{,}205$.
Внимание! В ролике на слайде 4 опечатка. Следует читать так:
$\displaystyle a:b=(2{,}1 \cdot 10^{3}):(1{,}4 \cdot 10^{-2})=(2{,}1:1{,}4) \cdot (10^{3}:10^{-2})=1{,}5 \cdot 10^{5}=150000$
$\displaystyle \frac{2{,}1 \cdot 10^{3}}{1{,}4 \cdot 10^{-2}}=\frac{2{,}1}{1{,}4} \cdot \frac{10^{3}}{10^{-2}}=1{,}5 \cdot10^{5}=150000$.
Видеоролик "Стандартный вид числа"
Задание 1:
Выполните действия с обыкновенными дробями: $\displaystyle -20\cdot \Big(\frac{3}{20}-\frac{2}{5}-\frac{1}{4} \Big)$.
Задание 2:
Выполните действия с десятичными дробями: $\displaystyle (0{,}48-0{,}24) \cdot 0{,}5+3{,}57:3{,}5$.
Варианты ответов:
Задание 3:
Вычислите: $\displaystyle \frac{4^7 \cdot 64}{16^4}$.
Задание 4:
Пусть $\displaystyle a=1{,}3 \cdot 10^8, \ b=2{,}6 \cdot 10^5$. Найдите $\displaystyle a : b$.
Задание 5:
Упростите: $\displaystyle \lvert -1 \rvert - \lvert 2-5 \rvert + \lvert 4-3 \rvert + \lvert -5-12 \rvert$.
Задание 6:
Сократить дробь: $\displaystyle \frac{\lvert 350 \rvert - \lvert -350 \rvert}{45 \cdot 655}$.
Задание 7:
Расположите в порядке убывания числовые выражения: $\displaystyle \frac{7^5}{7^3}, \ \ \lvert -50 \rvert, \ \ \frac{3{,}57}{0{,}07}$.
Выберете номер правильного ответа из предложенных ниже:
$\displaystyle 1$. $\displaystyle \frac{7^5}{7^3}, \ \ \lvert -50 \rvert, \ \ \frac{3{,}57}{0{,}07}$.
$\displaystyle 2$. $\displaystyle \lvert -50 \rvert, \ \ \frac{7^5}{7^3}, \ \ \frac{3{,}57}{0{,}07}$.
$\displaystyle 3$. $\displaystyle \frac{3{,}57}{0{,}07}, \ \ \lvert -50 \rvert, \ \ \frac{7^5}{7^3}$.
Задание 8:
На координатной прямой точки $\displaystyle A, \ B, \ C, \ D$ соответствуют числам $\displaystyle 0{,}508; \ 0{,}85; \ -0{,}05; \ 0{,}058$.

Какой точке соответствует число $\displaystyle 0{,}058$?
Укажите номер правильного ответа.
$\displaystyle 1) \ A; \ \ 2) \ B; \ \ 3) \ C; \ \ 4) \ D.$
Задание 9:
Установите соответствие между величинами и их возможными значениями: к каждому элементу из столбца "Величины" подберите соответствующий элемент из столбца "Значения".
ВЕЛИЧИНЫ:
А) рост взрослого человека
Б) толщина листа бумаги
В) протяженность автобусного маршрута
Г) высота башни
ЗНАЧЕНИЯ:
$\displaystyle 1) \ 36$ км
$\displaystyle 2) \ 42$ м
$\displaystyle 3) \ 0{,}2$ мм
$\displaystyle 4) \ 180$ см
В ответе запишите какую-нибудь одну последовательность цифр (для А, Б, В, Г соответственно) без пробелов, запятых и других дополнительных символов.
Задание 10:
На столбчатой диаграмме показано какое число учащихся математического кружка имеют определенный рост. Сколько учеников посещают кружок?
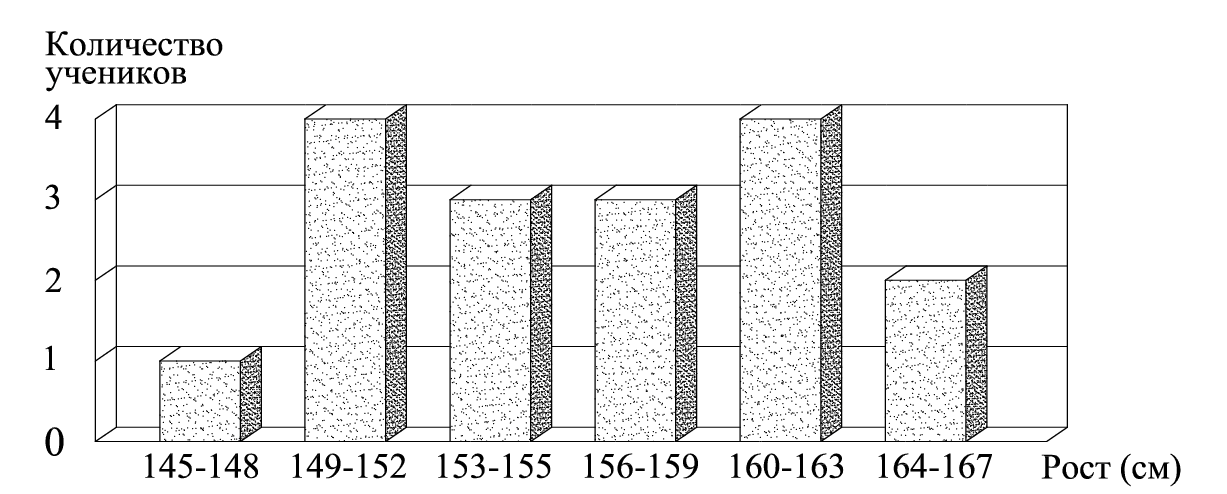
20 урок
Пример. Необходимо разместить в банке $\displaystyle 8000$ рулей на $\displaystyle 3$ года. Условия размещения вклада в трех банках приведены в таблице.

Найдите наибольший возможный доход в рублях, который может быть получен.
Капитализацией называется присоединение начисленных процентов к сумме вклада.
Решение. Определим возможный доход при размещении вклада в каждом из банков.
Банк "Взлет": $\displaystyle 8000 \cdot 1{,}5=12 000$. Возможный доход $\displaystyle 12 000-8000=4000$ рублей.
Банк "Стремление": $\displaystyle 8000 \cdot 1{,}15^3=8000 \cdot 1{,}520 875=12 167$. Возможный доход $\displaystyle 12 167-8000=4167$ рублей.
Банк "Надежда": $\displaystyle 8000 \cdot 0{,}17=1360$ рублей- доход за $\displaystyle 1$ год.
Доход за три года: $\displaystyle 1360 \cdot 3 =4080$ рублей.
Премия $\displaystyle 1$% от суммы вклада: $\displaystyle 8000 \cdot 0{,}01=80$ рублей.
Возможный доход за $\displaystyle 3$ года в банке "Надежда" составит $\displaystyle 4080+80=4160$ рублей.
Сравнивая возможный доход в каждом из трех банков, выбираем наибольший - $\displaystyle 4167$ рублей.
Ответ: $\displaystyle 4167$.
Видеоролик "Круги на клетчатой бумаге"
Задание 1:
Найдите значение выражения $\displaystyle \frac{\sqrt {20} \cdot \sqrt 8}{\sqrt {10}}$.
Задание 2:
Цена на элетроприбор была повышена на $\displaystyle 15$% и составила $\displaystyle 2875$ рублей. Сколько рублей стоил электроприбор до повышения цены?
Задание 3:
Найдите корень уравнения $\displaystyle \log_5(6-x) = \log_53$.
Задание 4:
Объем куба равен $\displaystyle 4$. Найдите объем другого куба, ребро которого в $\displaystyle 2$ раза больше ребра данного куба.
Задание 5:
При подготовке к экзамену студент выучил $\displaystyle 13$ билетов из $\displaystyle 20$. Найдите вероятность того, что студент знает ответ на случайно выбранный билет.
Варианты ответов:
Задание 6:
Найдите площадь $\displaystyle S$ половины круга радиуса $\displaystyle 4$ с центром в начале координат. В ответе укажите $\displaystyle \frac{S}{\pi}$.
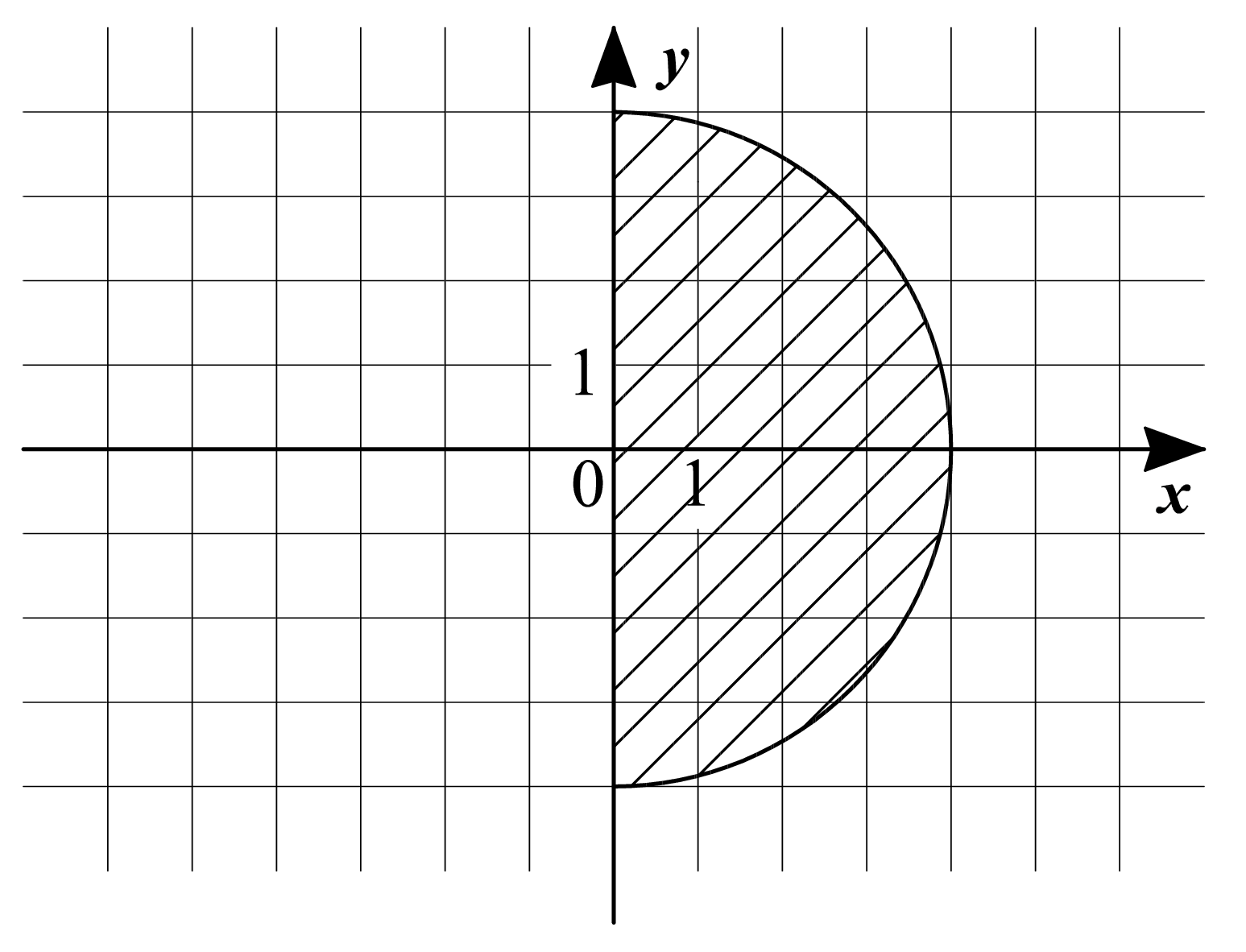
Задание 7:
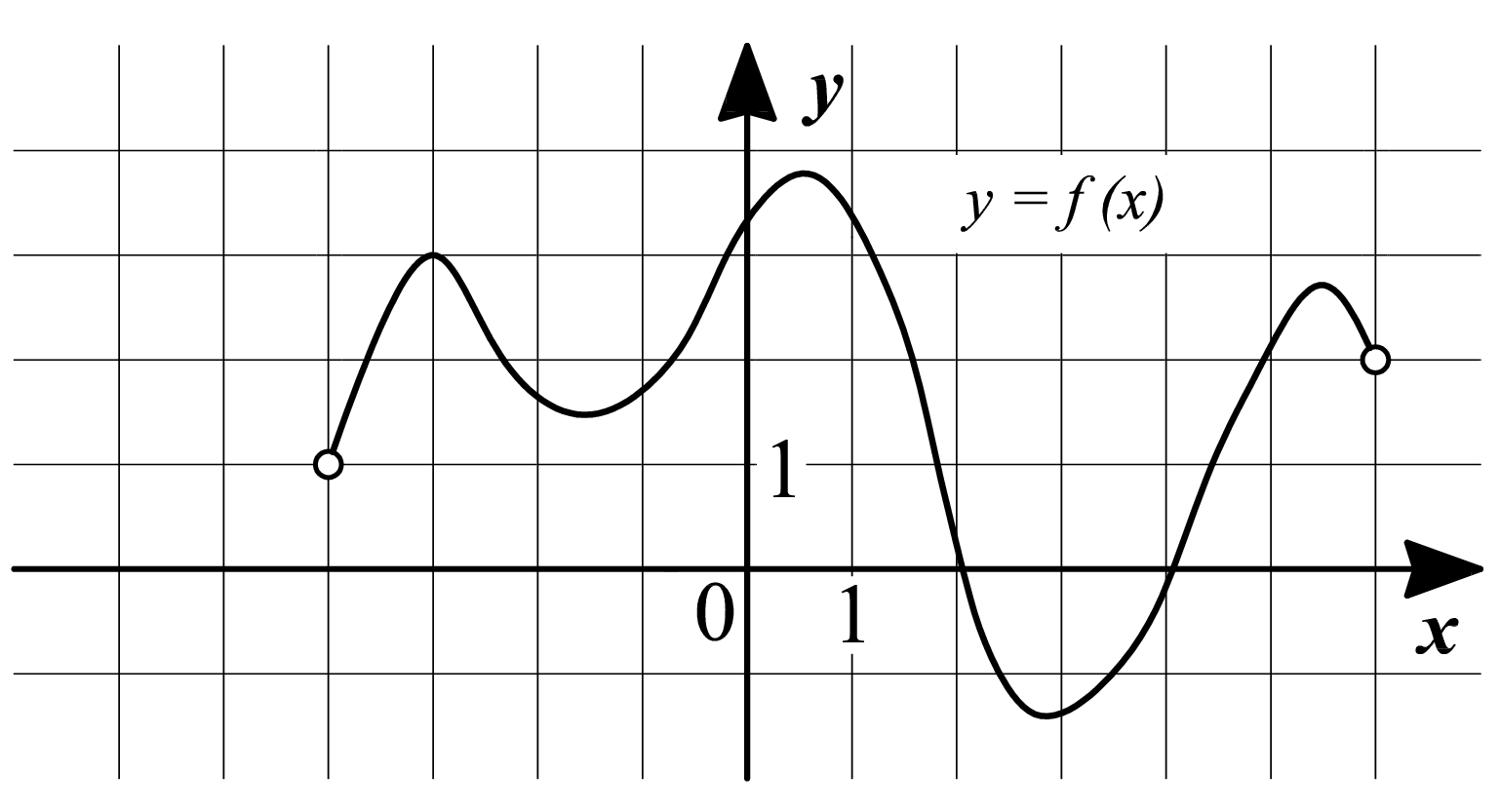
На рисунке изображен график функции $\displaystyle y=f(x)$. Найдите количество точек, в которых эта функция равна $\displaystyle 2$.
Задание 8:
В прямоугольном треугольнике $\displaystyle ABC$ с гипотенузой $\displaystyle AB=7$ тангенс угла $\displaystyle B$ равен $\displaystyle 2$. Найдите площадь треугольника.
Варианты ответов:
Задание 9:
Необходимо разместить в банке $\displaystyle 1$ миллион рулей на $\displaystyle 3$ года. Условия размещения вклада в трех банках приведены в таблице.

Найдите наибольший возможный доход в рублях, который может быть получен.
Капитализацией называется присоединение начисленных процентов к сумме вклада.
Задание 10:
На рисунке изображены график функции $\displaystyle y=f(x)$ и касательная к графику этой функции, проведенная в точке графика с абсциссой $\displaystyle a$. Найдите значение производной функции $\displaystyle y=f(x)$ в точке $\displaystyle a$.
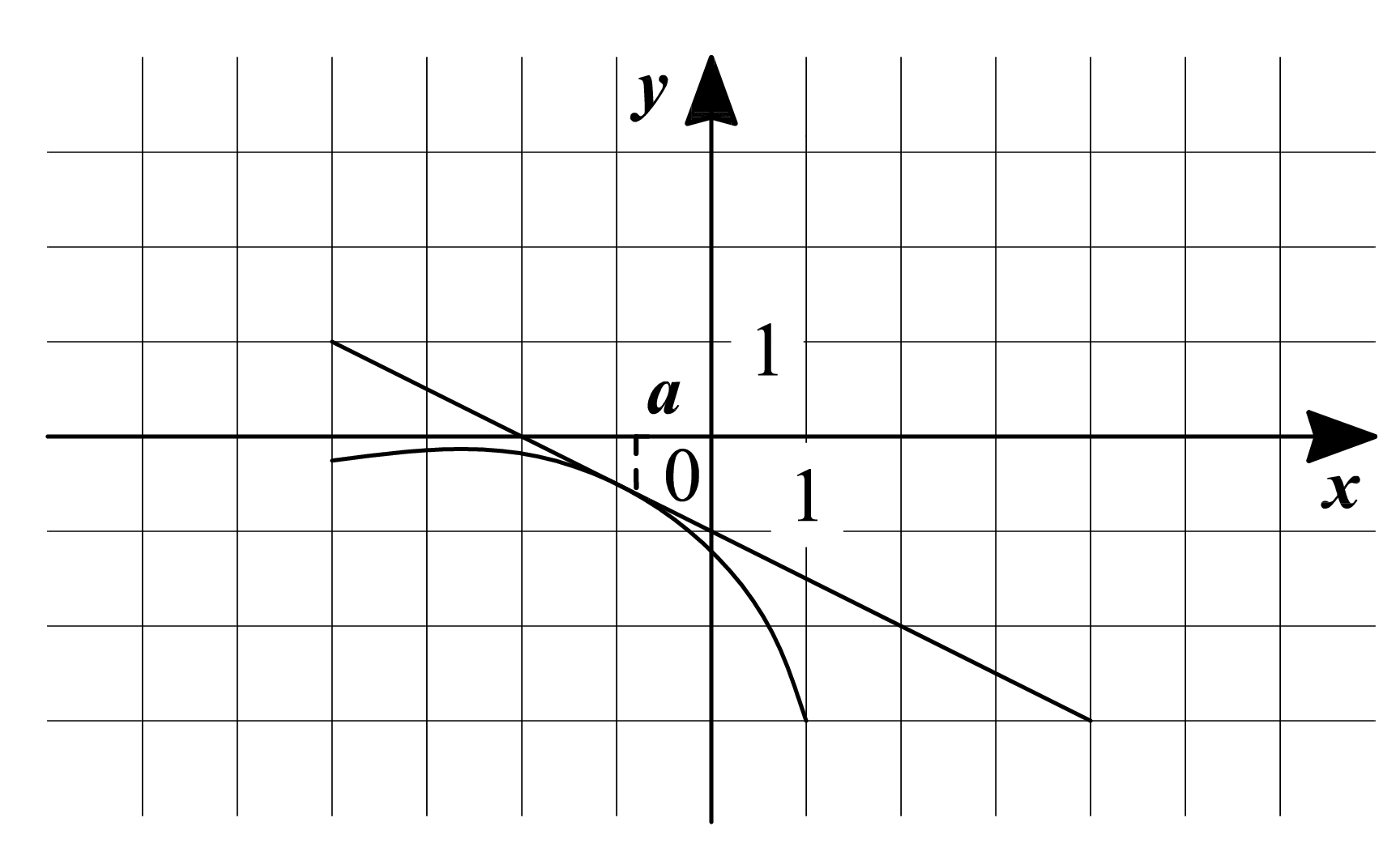
Варианты ответов:
![[Математический кружок]](/img/logo/header-ru-transparent-v5.png)