![Примеры уроков. Летний интенсив по математике — краткое повторение кружка 5 класса [Примеры уроков. Летний интенсив по математике — краткое повторение кружка 5 класса]](/img/theme/subjects/math-64.png) | Примеры уроков. Летний интенсив по математике — краткое повторение кружка 5 классаПримеры уроков. Летний интенсив по математике — краткое повторение кружка 5 класса |
Примеры уроков онлайн-курса «Летний интенсив»
Примеры уроков онлайн-курса «Летний интенсив»
1 урок
Теория:
Десятичная система счисления
Натуральные числа - для счёта предметов.
Это числа $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ \dots$
Ряд натуральных чисел бесконечен.
Цифры: $\displaystyle 0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.
Число $\displaystyle 10$ – основание системы счисления.
Счёт идёт десятками, сотнями, тысячами и так далее.
$\displaystyle 1$ десяток $\displaystyle = 10$ единиц
$\displaystyle 1$ сотня $\displaystyle = 10$ десятков
$\displaystyle 1$ тысяча $\displaystyle = 10$ сотен
Единица каждого следующего разряда в $\displaystyle 10$ раз больше единицы предыдущего разряда.
$\displaystyle 1$ миллион = $\displaystyle 1000000$
$\displaystyle 1$ миллиард = $\displaystyle 1000000000$
Разложение по разрядам:
$\displaystyle 2345 = 2 \cdot 10 \cdot 10 \cdot 10 + 3 \cdot 10 \cdot 10 + $ $\displaystyle 4 \cdot 10 + $ $\displaystyle 5 = $ $\displaystyle 2 \cdot 1000 + 3 \cdot 100 + 4 \cdot 10 + 5$.
Чётные числа делятся на $\displaystyle 2$, оканчиваются на чётную цифру $\displaystyle 0$, $\displaystyle 2$, $\displaystyle 4$, $\displaystyle 6$ или $\displaystyle 8$.
Нечётные числа не делятся на $\displaystyle 2$, оканчиваются на нечётную цифру $\displaystyle 1$, $\displaystyle 3$, $\displaystyle 5$, $\displaystyle 7$ или $\displaystyle 9$.
Натуральные числа, делящиеся на $\displaystyle 5$, оканчиваются цифрой $\displaystyle 0$ или $\displaystyle 5$.
Цифры в записи числа не повторяются, например: $\displaystyle 13579$.
Цифры в записи числа повторяются, например: $\displaystyle 32183$, $\displaystyle 28822$, $\displaystyle 55555$.
В двузначном числе $\displaystyle 53$ цифра десятков - $\displaystyle 5$, а цифра единиц - $\displaystyle 3$. Цифра единиц на $\displaystyle 2$ меньше, чем цифра десятков.
Задача
Сколько различных четырёхзначных чисел можно составить из цифр $\displaystyle 0$, $\displaystyle 1$, $\displaystyle 2$ и $\displaystyle 3$, если цифры в записи числа не повторяются?
Решение:
1 способ: запишем все возможные числа в порядке возрастания: $\displaystyle 1023$, $\displaystyle 1032$, $\displaystyle 1203$, $\displaystyle 1230$, $\displaystyle 1302$, $\displaystyle 1320$, $\displaystyle 2013$, $\displaystyle 2031$, $\displaystyle 2103$, $\displaystyle 2130$, $\displaystyle 2301$, $\displaystyle 2310$, $\displaystyle 3012$, $\displaystyle 3021$, $\displaystyle 3102$, $\displaystyle 3120$, $\displaystyle 3201$, $\displaystyle 3210$.
2 способ: первая цифра может быть любая из $\displaystyle 3$-х ($\displaystyle 1$, $\displaystyle 2$ или $\displaystyle 3$) - $\displaystyle 0$ записать нельзя; вторая цифра - не может быть такой же, как первая, но может быть $\displaystyle 0$, значит, $\displaystyle 3$ возможности, затем $\displaystyle 2$ возможности для предпоследней цифры и $\displaystyle 1$ возможность для постановки последней цифры.
$\displaystyle 3 \cdot 3 \cdot 2 \cdot 1 = 18$.
Двоичная система счисления
В двоичной системе счисления только две цифры $\displaystyle 0$ и $\displaystyle 1$.
С их помощью можно записать любое число.
Счёт ведётся двойками. За основание системы счисления принимается число $\displaystyle 2$.
Число $\displaystyle 2$ записывается в виде $\displaystyle 10_2$, читается "один-нуль".
Каждая единица следующего разряда в $\displaystyle 2$ раза больше предыдущей.
Числа от $\displaystyle 1$ до $\displaystyle 10$ записываются так:
$\displaystyle 1_2$, $\displaystyle 10_2$, $\displaystyle 11_2$, $\displaystyle 100_2$, $\displaystyle 101_2$, $\displaystyle 110_2$, $\displaystyle 111_2$, $\displaystyle 1000_2$, $\displaystyle 1001_2$, $\displaystyle 1010_2$.
Латинский алфавит ($\displaystyle 26$ букв):
$\displaystyle A,\ B,\ C,\ D,\ E,\ F,\ G,\ H,\ I,\ J,$
$\displaystyle K,\ L,\ M,\ N,\ O,\ P,\ Q,\ R,\ S,\ T,$
$\displaystyle U,\ V,\ W,\ X,\ Y,\ Z. $
Объёмные фигуры - куб, шар, прямоугольный параллелепипед, цилиндр.
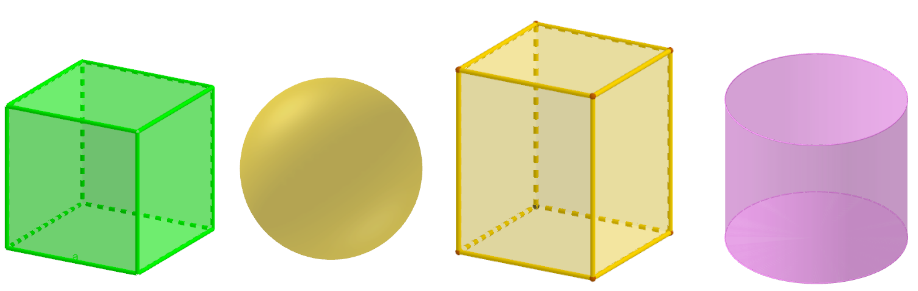
Плоские фигуры - квадрат, круг, треугольник, прямоугольник.

Учимся решать задачи
Задание 1:
Напишите наименьшее число, составленное из десяти различных цифр, делящееся на $\displaystyle 5$.
Задание 2:
Напишите число, состоящее из $\displaystyle 18$ тысяч, $\displaystyle 18$ сотен, $\displaystyle 18$ десятков и $\displaystyle 18$ единиц.
Задание 3:
Сколько различных пятизначных чисел можно составить из цифр $\displaystyle 0$, $\displaystyle 1$, $\displaystyle 2$, $\displaystyle 4$ и $\displaystyle 8$, если цифры в записи числа не повторяются?
Задание 4:
Как записывается число $\displaystyle 101101_2$ в десятичной системе счисления?
Задание 5:
Сколько нужно сделать распилов, чтобы распилить бревно на $\displaystyle 20$ частей?
Задание 6:
Во время прогулки по лесу Ваня через каждые $\displaystyle 10$ м находил гриб. Какой путь он проделал от первого гриба до последнего, если всего он нашёл $\displaystyle 20$ грибов? Дайте ответ в метрах.
Задание 7:
Сын вдвое моложе отца. Родился он, когда отцу было $\displaystyle 26$ лет. Сколько лет сыну? Дайте ответ в годах.
Задание 8:
Было $\displaystyle 12$ листов бумаги. Некоторые из них разрезали на три части. Всего стало $\displaystyle 26$ листов. Сколько листов бумаги разрезали?
Задание 9:
Задание 10:

Сколько кубиков нужно для построения фигуры?
20 урок
Теория:
Игры
Игры-шутки
Это игры, исход которых не зависит от того, как играют соперники.
Игры с симметрией
В таких играх выгодно отвечать на ход противника "симметричным" ходом.
Игры с выигрышными позициями
В таких играх следует искать выигрышную позицию и стремиться передать очередь невыгодного хода противнику.
Задача $\displaystyle 1$
На столе лежат $\displaystyle 30$ камешков. Два игрока по очереди берут $\displaystyle 1$, $\displaystyle 2$ или $\displaystyle 3$ камешка. Проигравшим считается тот, кто возьмёт со стола последние камешки. Докажите, что при правильной игре выигрывает начинающий.
Доказательство:
Выигрышная стратегия для первого игрока: первому игроку следует первым ходом взять один камешек, а в дальнейшем дополнять число камешков, взятых вторым игроком на последнем ходу, до $\displaystyle 4$.
Задача $\displaystyle 2$
Игра начинается с числа $\displaystyle 0$. За ход разрешается прибавить к имеющемуся числу любое натуральное число от $\displaystyle 1$ до $\displaystyle 9$. Выиграет тот, кто получит число $\displaystyle 100$. Кто и как выиграет при правильной игре?
Решение:
Выиграет второй. Второй игрок должен прибавлять такое число, чтобы в сумме получить число, делящееся на $\displaystyle 10$.
Ответ: выиграет второй при правильной игре.
Учимся решать задачи
Кендоку
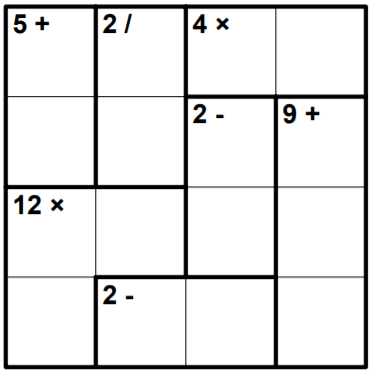
Разгадайте кендоку: заполните клетки числами от $\displaystyle 1$ до $\displaystyle 4$ включительно так, чтобы в каждой строке и в каждом столбце числа не повторялись. Число, которое записано в углу каждого выделенного блока - это результат сложения, вычитания, умножения или деления в этом блоке. Числа внутри блока могут повторяться.
Решение:
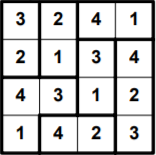
Задание 1:
Задание 2:
Задание 3:
Варианты ответов:
Задание 4:

Мысленно сверните куб из развёртки и определите, какая грань является нижней, если верхняя грань синяя?
Варианты ответов:
Задание 5:
Задание 6:
На столе лежат $\displaystyle 25$ камешков. Два игрока по очереди берут $\displaystyle 1$ или $\displaystyle 2$ камешка. Проигравшим считается тот, кто возьмёт со стола последние камешки. Кто выиграет при правильной игре?
Варианты ответов:
Задание 7:
В ящике $\displaystyle 15$ жёлтых шаров, $\displaystyle 20$ чёрных, $\displaystyle 25$ синих и $\displaystyle 30$ красных. На ощупь шары неотличимы друг от друга. Шары вынимают из ящика в темноте. Какое наименьшее число шаров нужно вынуть, чтобы среди них обязательно оказалось $\displaystyle 5$ шаров одного цвета?
Задание 8:
В комнате стоят табуретки и стулья. У каждой табуретки $\displaystyle 3$ ноги, у каждого стула $\displaystyle 4$ ноги. Когда на всех табуретках и стульях сидят люди, в комнате всего $\displaystyle 27$ ног. Сколько стульев в комнате?
Задание 9:
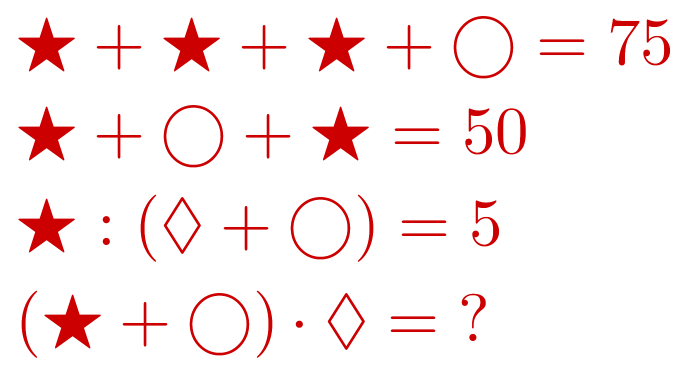
Какое число надо записать вместо вопросительного знака?
Задание 10:
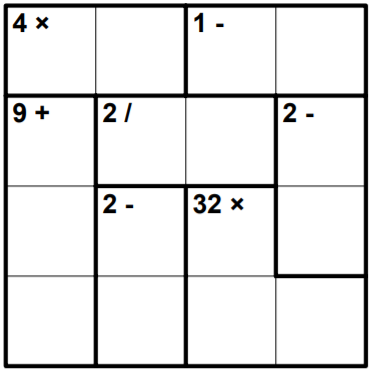
Разгадайте кендоку: заполните клетки числами от $\displaystyle 1$ до $\displaystyle 4$ включительно так, чтобы в каждой строке и в каждом столбце числа не повторялись. Число, которое записано в углу каждого выделенного блока - это результат сложения, вычитания, умножения или деления в этом блоке. Числа внутри блока могут повторяться.
Какое число будет записано в нижней строке в угловой клетке слева?
![[Математический кружок]](/img/logo/header-ru-transparent-v5.png)