МетаШкола - Примеры уроков - Геометрия 8 класс

1 урок

Теория:

Многоугольник

Многоугольник – фигура, составленная из отрезков так, что смежные отрезки не лежат на одной прямой, а несмежные отрезки не имеют общих точек.

Точки $\displaystyle A,\ B,\ C,\ D,\ E$ – вершины многоугольника.

Отрезки $\displaystyle AB,\ BC,\ CD,\ DE,\ EA$ – стороны многоугольника.

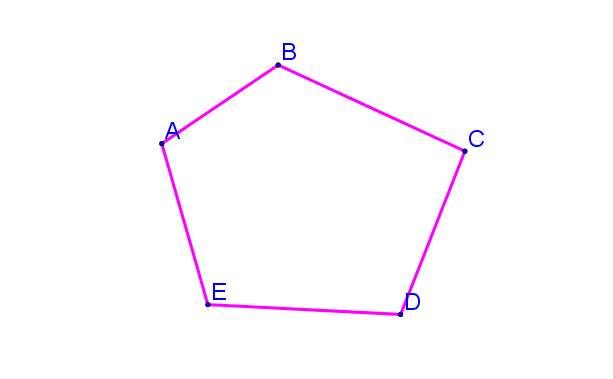
Периметр многоугольника – сумма длин всех сторон.

Многоугольник с $\displaystyle n$ вершинами называется $\displaystyle n$-угольником; он имеет $\displaystyle n$ сторон.

Две вершины многоугольника, принадлежащие одной стороне, называются соседними.

Диагональ многоугольника – отрезок, соединяющий любые две несоседние вершины.

Любой многоугольник разделяет плоскость на две части, одна из которых называется внутренней, а другая – внешней областью многоугольника.

Фигуру, состоящую из сторон многоугольника и его внутренней области, также называют многоугольником.

Учимся решать задачи

Задание 1:

Начертите произвольный пятиугольник. Постройте все диагонали. Может ли общее число диагоналей быть равным $\displaystyle 5$?

Варианты ответов:

нетда

Задание 2:

Всегда ли площадь шестиугольника больше, чем площадь пятиугольника?

Варианты ответов:

данет

Задание 3:

Первая сторона пятиугольника в $\displaystyle 2$ раза больше второй, третья - равна сумме первой и второй, четвёртая - на $\displaystyle 2$ см больше второй, пятая - на $\displaystyle 5$ см меньше третьей. Найдите периметр пятиугольника, если известно, что длина пятой стороны - $\displaystyle 13$ см.

Варианты ответов:

$\displaystyle 55$ см$\displaystyle 53$ см$\displaystyle 59$ см$\displaystyle 54$ см$\displaystyle 57$ см

Задание 4:

Начертите равносторонний четырёхугольник. Постройте все диагонали. На сколько частей разделена плоскость?

Варианты ответов:

$\displaystyle 4$$\displaystyle 5$$\displaystyle 6$$\displaystyle 3$$\displaystyle 2$

Задание 5:

Можно ли построить четырёхугольник, у которого две соседние стороны по $\displaystyle 3$ см, а две другие - по $\displaystyle 6$ см?

Варианты ответов:

данет

Задание 6:

Постройте прямоугольник $\displaystyle ABCD$, проведите диагональ $\displaystyle AC$, точка $\displaystyle O$ - середина $\displaystyle AC$, $\displaystyle OE$ - перпендикуляр к $\displaystyle AD$, $\displaystyle F$ - середина $\displaystyle ED$. Сравните площади $\displaystyle \triangle AOE$ и $\displaystyle \triangle OEF$. Какой из этих треугольников имеет большую площадь?

Варианты ответов:

площади равны$\displaystyle \triangle OEF$$\displaystyle \triangle AOE$

Задание 7:

Можно ли равносторонний шестиугольник разделить на равные треугольники двумя диагоналями?

Варианты ответов:

нетда

40 урок

Теория:

Средняя линия трапеции

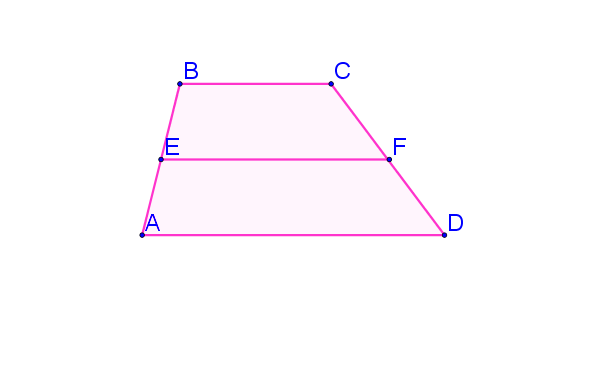
Средней линией трапеции называется отрезок, соединяющий середины её боковых сторон.

Теорема. Средняя линия трапеции параллельна основаниям и равна их полусумме.

Учимся решать задачи

Задание 1:

Боковые стороны трапеции равны $\displaystyle 12$ см и $\displaystyle 14$ см, периметр равен $\displaystyle 56$ см. Найдите среднюю линию трапеции.

Варианты ответов:

$\displaystyle 16$ см$\displaystyle 15$ см$\displaystyle 18$ см$\displaystyle 25$ см$\displaystyle 26$ см

Задание 2:

Верно ли утверждение: средняя линия трапеции проходит через середины диагоналей?

Варианты ответов:

данет

Задание 3:

Дана равнобедренная трапеция $\displaystyle ABCD$. $\displaystyle BO \perp AD$, $\displaystyle DO=8$ см. Найдите среднюю линию трапеции.

Варианты ответов:

$\displaystyle 6$ см$\displaystyle 16$ см$\displaystyle 8$ см$\displaystyle 4$ см$\displaystyle 10$ см

Задание 4:

Дана трапеция $\displaystyle ABCD$ с основаниями $\displaystyle AD$ и $\displaystyle BC$. Выразите вектор $\displaystyle \vec{AD} - \vec{CD}$ через векторы $\displaystyle \vec{a} =\vec{AB}$ и $\displaystyle \vec{b} =\vec{CB}$

Варианты ответов:

$\displaystyle \vec{b} - \vec{a}$$\displaystyle \vec{a} - \vec{b}$$\displaystyle \vec{a} + \vec{b}$$\displaystyle \vec{b} + \vec{a}$$\displaystyle 2\vec{a} - \vec{b}$

Задание 5:

Боковая сторона равнобедренной трапеции равна $\displaystyle 24$ см, а средняя линия делится диагональю на два отрезка, которые равны $\displaystyle 5,\!5$ см и $\displaystyle 17,\!5$ см. Найдите угол при большем основании трапеции.

Варианты ответов:

$\displaystyle 20^\circ$$\displaystyle 60^\circ$$\displaystyle 30^\circ$$\displaystyle 90^\circ$$\displaystyle 45^\circ$

Задание 6:

Верно ли утверждение: отрезок, соединяющий середины диагоналей трапеции, параллелен её основаниям и равен полуразности оснований?

Варианты ответов:

нетда

Задание 7:

В трапеции $\displaystyle ABCD$ основание $\displaystyle AD$ в $\displaystyle 3$ раза больше основания $\displaystyle BC$. Выразите вектор $\displaystyle \vec{BC}$ через векторы $\displaystyle \vec{BA}=a$ и $\displaystyle \vec{CD}=b$.

Варианты ответов:

$\displaystyle \frac{1}{2}\vec{b} - \frac{1}{2}\vec{a}$$\displaystyle \frac{1}{2}\vec{b} - \vec{a}$$\displaystyle \vec{b} - \frac{1}{2}\vec{a}$$\displaystyle \frac{1}{2}\vec{a} + \frac{1}{2}\vec{b}$$\displaystyle \vec{a} + \vec{b}$

Примеры уроков. Геометрия 8 класс

Примеры уроков. Геометрия 8 класс

Примеры уроков онлайн-курса по школьной программе

Примеры уроков онлайн-курса по школьной программе

1 урок

40 урок