МетаШкола - Примеры уроков - Геометрия 7 класс

1 урок

Теория:

Точки, прямые, отрезки

Через любые две точки можно провести прямую, и притом только одну.

Две прямые либо имеют только одну общую точку,

либо не имеют общих точек.

Отрезок – часть прямой, ограниченная двумя точками.

Концы отрезка – точки, ограничивающие отрезок.

Попарно пересекающиеся прямые - это значит, что у любых двух прямых есть общая точка.

Учимся решать задачи

Задание 1:

Проведите прямую и отметьте на ней $\displaystyle 4$ точки. Сколько отрезков получилось на прямой?

Задание 2:

На прямой отметьте последовательно точки $\displaystyle M,\ N,\ P,\ S,\ T$. Сколько отрезков, на которых не лежит точка $\displaystyle S$?

Задание 3:

Отметьте точки $\displaystyle A,\ B,\ C,\ D$ и $\displaystyle E$ так, чтобы точки $\displaystyle A,\ B,\ C,\ D$ лежали на одной прямой, а точка $\displaystyle E$ не лежала на ней. Через каждые две точки проведите прямую. Сколько получилось прямых?

Задание 4:

Можно ли начертить две пересекающиеся прямые и расположить на них два не пересекающихся отрезка так, чтобы точка пересечения прямых принадлежала одному из них?

Варианты ответов:

ДаНет

Задание 5:

Сколько точек надо взять между точками $\displaystyle A$ и $\displaystyle B$, чтобы вместе с отрезком $\displaystyle AB$ получилось десять различных отрезков?

Задание 6:

Даны четыре точки, никакие три из них не лежат на одной прямой. Можно ли провести шесть прямых так, чтобы каждая из этих прямых проходила ровно через две заданные точки?

Варианты ответов:

НетДа

Задание 7:

Сколько точек пересечения могут иметь четыре попарно пересекающиеся прямые? Не допускается пересечение трёх или четырёх прямых в одной точке. Каждая прямая пересекает три другие прямые.

38 урок

Теория:

Построение треугольника по трём элементам

$\displaystyle 1)$ По двум сторонам и углу между ними.

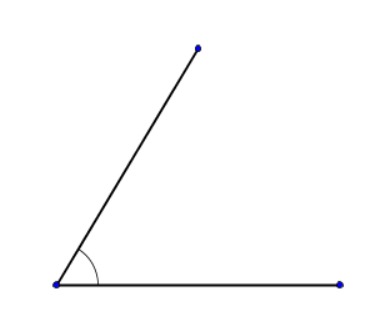
$\displaystyle 2)$ По стороне и двум прилежащим к ней углам.

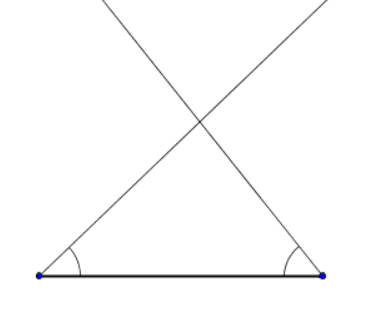
$\displaystyle 3)$ По трём сторонам.

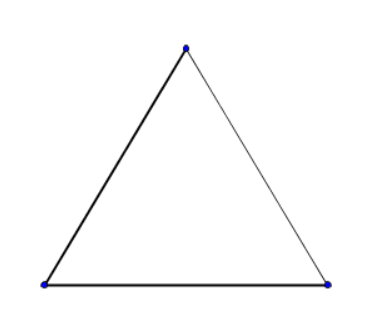
Учимся решать задачи

Задание 1:

Что представляет собой множество всех точек плоскости, находящихся на данном расстоянии от данной прямой?

Варианты ответов:

Две прямые, параллельные данной прямой и расположенные на данном расстоянии по разные стороны от неёОкружность, радиус которой равен данному расстояниюДве прямые, параллельные данной прямой, расстояние между которыми равно данному расстояниюПрямая, параллельная данной прямой и расположенная на данном расстоянии от неёДве прямые, перпендикулярные данной прямой и расположенные на данном расстоянии

Задание 2:

Можно ли построить треугольник по катету и прилежащему к нему острому углу?

Варианты ответов:

ДаНет

Задание 3:

В равнобедренном $\displaystyle \triangle ABC$ с основанием $\displaystyle AC$, равным $\displaystyle 27$ см, внешний угол при вершине $\displaystyle B$ равен $\displaystyle 60^{\circ}$. Найдите расстояние от вершины $\displaystyle C$ до прямой $\displaystyle AB$.

Варианты ответов:

$\displaystyle 12$ см$\displaystyle 9$ см$\displaystyle 13{,}5$ см$\displaystyle 27$ см$\displaystyle 18$ см

Задание 4:

В $\displaystyle \triangle ABC$ $\displaystyle \angle A = 70^{\circ}$, $\displaystyle \angle B = 80^{\circ}$, $\displaystyle BE$ - биссектриса, $\displaystyle EC=8$ см. Найдите расстояние от точки $\displaystyle E$ до прямой $\displaystyle AB$. Дайте ответ в сантиметрах.

Задание 5:

Через середину стороны $\displaystyle BC$ $\displaystyle \triangle ABC$ проведена прямая, перпендикулярная к $\displaystyle BC$, пересекающая $\displaystyle AB$ в точке $\displaystyle D$, $\displaystyle AB=18$ см, периметр $\displaystyle \triangle ADC$ равен $\displaystyle 26$ см. Найдите $\displaystyle AC$. Дайте ответ в сантиметрах.

Задание 6:

В прямоугольном $\displaystyle \triangle ABC$ $\displaystyle \angle C$ - прямой, биссектрисы $\displaystyle CD$ и $\displaystyle AE$ пересекаются в точке $\displaystyle O$. $\displaystyle \triangle AOC = 105^{\circ}$. Найдите острые углы $\displaystyle \triangle ABC$.

Варианты ответов:

$\displaystyle 30^{\circ}$ и $\displaystyle 60^{\circ}$$\displaystyle 35^{\circ}$ и $\displaystyle 55^{\circ}$$\displaystyle 40^{\circ}$ и $\displaystyle 50^{\circ}$$\displaystyle 10^{\circ}$ и $\displaystyle 80^{\circ}$$\displaystyle 20^{\circ}$ и $\displaystyle 70^{\circ}$

Задание 7:

Верно ли утверждение: основание равнобедренного треугольника параллельно биссектрисе одного из внешних углов?

Варианты ответов:

ДаНет

Примеры уроков. Геометрия 7 класс

Примеры уроков. Геометрия 7 класс

Примеры уроков онлайн-курса по школьной программе

Примеры уроков онлайн-курса по школьной программе

1 урок

38 урок