Примеры уроков. ЕГЭ по математике (профильный уровень) для 10-11 классов

Взаимное расположение прямых в пространстве

Две различные  прямые в пространстве могут быть:

• параллельны (в таком случае существует и притом единственная плоскость, их содержащая, а угол между этими прямыми равен $\displaystyle 0^\circ$);
• пересекаться (в таком случае существует и притом единственная плоскость, их содержащая, а угол между этими прямыми вычисляется в этой плоскости);
• скрещиваться (в таком случае не существует плоскости, содержащей одновременно обе эти прямые, а угол между скрещивающимися прямыми находят с помощью параллельного переноса одной из прямых до пересечения со второй прямой).

Часто при нахождении угла между прямыми в пространстве используют теорему косинусов для треугольника, две стороны которого находятся на указанных прямых, или прямых, параллельных указанным.

Теорема косинусов: Для треугольника $\displaystyle ABC$ верно $\displaystyle BC^2=AB^2+AC^2-2 \cdot AB \cdot AC \cdot \cos \angle BAC.$

Перпендикулярность прямой и плоскост

Определение: прямая $\displaystyle a$ перпендикулярна плоскости $\displaystyle \alpha,$ если прямая $\displaystyle a$ перпендикулярна любой прямой, содержащейся в плоскости $\displaystyle \alpha:$ $\displaystyle a \perp \alpha.$

Признак перпендикулярности прямой и плоскости: если прямая перпендикулярно двум пересекающимся прямым, содержащимся в плоскости $\displaystyle \alpha,$ то прямая $\displaystyle a$ перпендикулярна плоскости $\displaystyle \alpha.$

Напоминание: в задачах по геометрии на доказательство можно использовать свойства или определение (например, того, что некоторая прямая $\displaystyle a$ перпендикуляра некоторой плоскости $\displaystyle \alpha$) в том случае, когда факт (например, что $\displaystyle a \perp \alpha$) известен из условия или получен по ходу решения, например, с помощью признака. Если же в условии задачи не дано, что определённая прямая $\displaystyle a$ перпендикуляра определённой плоскости и в решении не используется признак, по которому можно утверждать, что это так, то пользоваться свойствами или определением недопустимо (это будет грубой ошибкой).

Через любую точку пространства можно провести прямую, и притом единственную, перпендикулярную данной плоскости.

Если точка $\displaystyle A$ не принадлежит плоскости $\displaystyle \alpha,$ то проведение такой прямой называют опущением или проведением перпендикуляра на указанную плоскость из точки $\displaystyle A$ на плоскость $\displaystyle \alpha,$ а прямую, проходящую через точку $\displaystyle A$ и точку $\displaystyle H$ пересечения перпендикуляра и плоскости (основания перпендикуляра) называют проекцией этой прямой на плоскость $\displaystyle \alpha.$

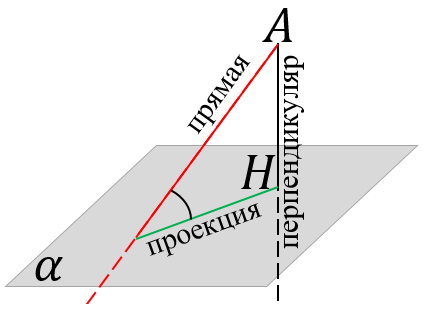
Взаимное расположение прямой и плоскости, угол между прямой и плоскостью

Прямая и плоскость могут быть:

• параллельны (в таком случае угол между ними равен $\displaystyle 0^\circ$);
• плоскость может содержать прямую (в таком случае угол между ними также равен $\displaystyle 0^\circ$);
• пересекаться и быть перпендикулярными (в таком случае угол между ними равен $\displaystyle 90^\circ$);
• пересекаться и не быть перпендикулярными (в таком случае угол между ними углу между этой прямой и её проекцией на эту плоскость).

Часто для нахождения угла между прямой и плоскостью используют теорему о трёх перпендикулярах.

Теорема о трёх перпендикулярах

Если через некоторую точку вне плоскости $\displaystyle \alpha$ проведены перпендикуляр $\displaystyle h$ к плоскости $\displaystyle \alpha$ и прямая $\displaystyle a$ - наклонная к плоскости $\displaystyle \alpha,$ прямая $\displaystyle b$ является проекцией прямой $\displaystyle a$ на плоскости $\displaystyle \alpha,$ и в плоскости $\displaystyle \alpha$ содержится некоторая прямая $\displaystyle c,$ то:

если проекция $\displaystyle b$ перпендикулярна прямой $\displaystyle c,$ то и наклонная $\displaystyle a$ перпендикулярна прямой $\displaystyle c;$ 

и обратно: если наклонная $\displaystyle a$ перпендикулярна прямой $\displaystyle c,$ то и проекция $\displaystyle b$ перпендикулярна прямой $\displaystyle c.$

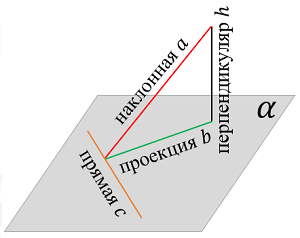
Взаимное расположение двух плоскостей

Две плоскости в пространстве могут быть параллельны или пересекаться.

Признак параллельности двух плоскостей

Если две пересекающиеся прямые, лежащие в одной плоскости, соответственно параллельны двум пересекающимся прямым, лежащим в другой плоскости, то такие плоскости параллельны.

Свойства параллельных плоскостей

Если две параллельные плоскости пересекаются третьей плоскостью, то прямые пересечения плоскостей параллельны;

отрезки параллельных прямых, отсекаемые параллельными плоскостями, равны между собой.

Свойства параллельных плоскостей необходимы при решении задач, в которых присутствуют призмы, в том числе параллелепипеды или цилиндры, так как при проведения сечения многогранника, отрезки сечения, лежащего в параллельных гранях, будут параллельны друг другу.

Угол между плоскостями

Если две различные плоскости, например, $\displaystyle \alpha$ и $\displaystyle \beta$ не параллельны, то есть имеют хотя бы одну общую точку, тогда их пересечением является прямая, например $\displaystyle c,$ которая делит каждую из плоскостей на две полуплоскости.  Фигура, содержащая общую прямую этих двух плоскостей и по одной полуплоскости от каждой из плоскостей называется двугранным углом.

Если из некоторой точки $\displaystyle O$ на прямой $\displaystyle c$ провести в указанных полуплоскостях двугранного угла лучи $\displaystyle OA$ и $\displaystyle OB$ где $\displaystyle A \in \alpha, OA \perp c$ и $\displaystyle B \in \beta, OB \perp c,$ то угол, образованный этими лучами, называется линейным углом двугранного угла между плоскостями $\displaystyle \alpha$ и $\displaystyle \beta.$

Угол между плоскостями равен наименьшему (острому или прямому) линейному углу двугранных углов между этими плоскостями. 

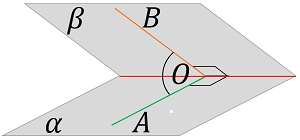
Для нахождения угла между плоскостями часто используют теорему о трёх перпендикулярах (см. выше). А в случае, когда требуется доказать, что угол между двумя плоскостями равен $\displaystyle 90^\circ,$ то есть две плоскости перпендикулярны, можно использовать признак перпендикулярности двух плоскостей:

Признак перпендикулярности двух плоскостей

Если одна из двух плоскостей пересекает прямую, перпендикулярную другой плоскости, то такие плоскости перпендикулярны.

Напоминание: в задачах по геометрии на доказательство можно использовать свойства или определение в том случае, когда факт известен из условия или получен по ходу решения, например, с помощью признака. Если же в условии задачи факт не указан и в решении не используется признак, по которому можно утверждать, что это так, то пользоваться свойствами или определением недопустимо (это будет грубой ошибкой).