Интернет-кружки /
Физика /
7 класс /
Примеры

Интернет-кружок по физике, 7 класс, примеры

Примерные серии задач интернет-кружка

1 серия (сентябрь) учебного года 2024-2025

Слово "физика" происходит от греческого слова "физюс", что означает природа.

Как вступление к занятиям в нашем кружке мы предлагаем прочитать ответы на вопросы, которые задали ученому-физику дети, еще не изучавшие физику в школе. Это поможет вам получить представление о том, что такое физика, и о том, как рассуждают ученые-физики. Возможно, многое из того, о чем рассказывается в ответах, вам покажется не до конца понятным, ведь для подробного ответа на каждый из этих вопросов можно написать отдельную толстую книгу.

На вопросы детей отвечает доктор физико-математических наук А.И. Шехтман.

1. Почему вы занимаетесь физикой?

Если отвечать одной фразой, то я бы сказал так: я занимаюсь физикой потому, что это интересно. Физика - это наука, которая изучает самые основные законы природы, описывающие, как устроен мир, в котором мы живём. Задавать вопросы природе (то есть проводить физические эксперименты), получать на них ответы и разбираться, что эти ответы означают - это действительно интересно, я в этом убедился за 30 лет работы физиком-экспериментатором.

2. Бывают ли инопланетяне?

Ответ на этот вопрос пока неизвестен. Непосредственно инопланетян никто не видел, хотя есть люди, которые объясняют некоторые необычные явления природы или факты истории вмешательством пришельцев с других планет. Серьёзные учёные занимаются поиском реальных фактов, которые подтвердили бы наличие внеземных цивилизаций. Например, сейчас интенсивно ищут другие планеты с условиями, пригодными для зарождения жизни. Планет таких найдено много десятков, однако пока никаких признаков даже жизни (не говоря о разумной жизни) на этих планетах не обнаружено. Но работа продолжается. Было бы, конечно, очень здорово найти во Вселенной братьев по разуму. В то же время есть соображения, которые ставят под сомнение существование других разумных цивилизаций - если бы они были, то они бы с нами связались или как-то проявили бы себя. Поскольку этого до сих пор не произошло - видимо, мы во Вселенной одиноки. Но будущее покажет, как же обстоит дело на самом деле.

3. Почему облака не падают на землю?

Облака состоят из очень мелких капелек воды, которые падают на землю очень медленно, из-за трения о воздух. Обычно облака образуются в тех местах, где есть восходящий поток тёплого воздуха, и это движение воздуха вверх не даёт образовавшимся мелким капелькам воды упасть. Однако, когда капельки начинают сливаться в более крупные, они начинают падать, и идёт дождь. Так что облака падают на землю в виде дождя, снега или града.

4. Почему в космосе нет воздуха, а на Земле есть воздух?

Воздух вокруг Земли образовался в результате выброса газа из вулканов, и он не улетает в космическое пространство благодаря притяжению Земли. Планеты размером с Землю или более крупные, как правило, имеют атмосферу, а маленькие планеты и спутники (например, Луна, Меркурий), на которых вулканическая деятельность давно прекратилась, не в состоянии удержать свою атмосферу, и она улетучилась в космос. В космосе же места очень много, а вещества очень мало, поскольку всё вещество из-за гравитационного притяжения сконцентрировано в небольших объектах - звёздах и планетах, между которыми в основном пустота и очень мало вещества.

5. Откуда появилась Земля?

Земля образовалась из космической пыли, которая собралась вместе благодаря гравитационному притяжению. А космическая пыль образовалась при взрывах звёзд. Когда звезда образуется, она состоит из водорода (это самый простой элемент). При образовании звезды она сжимается из-за гравитационного притяжения, разогревается, и в ней начинается термоядерная реакция - образование более тяжёлых химических элементов из водорода. Эта реакция обеспечивает высокую температуру звезды, благодаря чему она стабильно светится в течение нескольких миллиардов лет, но постепенно ядерное горючее заканчивается, и в какой-то момент происходит сжатие звезды и взрыв, при котором наработанные тяжёлые элементы выбрасываются в окружающее пространство в виде космической пыли. Потом на этом месте из водорода может образоваться другая звезда, а из космической пыли - планета, которая крутится вокруг этой звезды. Видимо, таким путём и образовалась Земля. Однако есть особенности Земли, которые трудно объяснить такой моделью (например, размер и скорость вращения Луны вокруг Земли). Поэтому существуют более сложные теории. Например, одна из таких теорий предполагает, что в первоначально образовавшуюся из космической пыли холодную Землю врезалась другая планета, в результате чего произошёл взрыв, и образовались Земля и Луна. У этой новой Земли сердцевина была очень горячей (и остаётся до сих пор), благодаря чему возникла интенсивная вулканическая деятельность, образовалась атмосфера, и возникла жизнь.

6. Что такое солнечное затмение?

Это такое красивое явление природы, когда Луна проходит между Солнцем и Землёй и отбрасывает на поверхность Земли тень. В результате наблюдатели, находящиеся в этой тени, видят, как в ясный день на Солнце наползает какой-то невидимый круглый объект и постепенно закрывает Солнце. Сначала Солнце приобретает форму серпа, потом он сужается, и в какой-то момент Солнце полностью закрывается чёрным диском Луны, на несколько минут наступает темнота, и на небе становятся видны звёзды. Через несколько минут эта полная фаза солнечного затмения заканчивается, и Солнце снова появляется сначала в виде серпа, а потом принимает свой обычный вид. Ширина лунной тени на поверхности Земли довольно небольшая (около

100

километров), поэтому полное солнечное затмение наблюдается каждый раз только вдоль узкой полосы на поверхности Земли. При этом в остальных местах можно видеть частичное солнечное затмение - Солнце принимает форму серпа, но полностью не закрывается. В каждом отдельно взятом месте полное солнечное затмение случается примерно раз в

100

лет. Однако мне, например, повезло, и я за свою жизнь видел полное солнечное затмение

3

раза (в разных местах): в

1960

году в Саратове, потом в

1986

году в Новосибирске и в

1999

году во Франции.

7. Почему люди не могут жить вечно?

Как известно, люди произошли в результате эволюции от животных (от обезьян), поэтому жизненный цикл человека подчиняется тем же законам, что и у животных. А в животном мире главная цель - выживание вида, а не отдельного живого существа. Конечно, борьба отдельного существа за выживание тоже существенна, но только для того, чтобы дать потомство, передав ему все свои наследственные признаки и тем самым продолжив жизнь своего вида. Безжалостная борьба за существование выбрала продолжительность жизни отдельного существа, наиболее оптимальную с точки зрения выживания вида. Эта продолжительность жизни различна у разных видов - есть насекомые, которые живут один день, и есть деревья, которые живут 3000 лет. Видимо, для выживания вида более выгодно, чтобы каждое существо жило ограниченное время, а потом умирало, дав жизнь новым поколениям существ того же вида. Люди унаследовали свою смертность от животных. Однако у людей появился новый способ передать свой опыт следующим поколениям - язык, письменность, искусство, наука. И поэтому древний человек, нарисовавший прекрасные рисунки на стенах пещеры, хотя и умер много тысяч лет назад, но сумел передать нам, своим потомкам, частичку своей души.

Для решения задач первой серии вам не потребуется никаких специальных знаний по физике.

Решить некоторые из задач помогут знания, полученные ранее на уроках математики, природоведения и окружающего мира.

___________________________

К задаче 3.

Конспект решения

Пусть

v_{п}

t_{п}

- скорость и время пассажира по неподвижному эскалатору

$v_{э}$ - скорость эскалатора

$t_{э}$ - столько времени поднимает эскалатор стоящего на нём пассажира

$l$ - длина подъёма

$t_{э + п}$ - время подъёма по движущемуся эскалатору, это нужно найти.

$t_{э} = \frac{l}{v_{э}}$

$t_{п} = \frac{l}{v_{п}}$

$t_{э + п} = \frac{l}{v_{э} + v_{п}}$

Выразим из двух уравнений скорости:

$v_{э} = \frac{l}{t_{э}}$ $v_{п} = \frac{l}{t_{п}}$

и подставим их в выражение для $t_{э + п}$ :

$t_{э + п} = \frac{l}{\frac{l}{t_{э}} + \frac{l}{t_{п}}} = \frac{l}{\frac{l \cdot t_{п} + l \cdot t_{э}}{t_{э} \cdot t_{п}}} = \frac{t_{э} \cdot t_{п}}{(t_{п} + t_{э})}$

Подставляем числа:

$t_{э + п} = \frac{40 с \cdot 120 с}{40 с + 120 с} = 30$

Задание 1:

Известно, что на фотографии растущая Луна.

Можно ли сказать, в каком полушарии сделана эта фотография?

Выберите вариант ответа:

Фотография сделана в северном полушарии.Фотография сделана в южном полушарии.Мы не можем сказать, в каком полушарии сделана фотография.

Указание.

Прочитайте отрывок из книги Я. Перельмана "Занимательная астрономия"

"Молодой или старый месяц?"

Загрузить Perelman_astr.pdf

Задание 2:

Два велосипедиста выехали одновременно навстречу друг другу из двух поселков, расстояние между которыми $40$ км.
Скорость первого велосипедиста $10$ км/ч, а второго - $14$ км/ч.
Первый велосипедист взял с собой собаку. Собака сразу побежала навстречу второму велосипедисту, встретила его, и побежала обратно навстречу своему хозяину. Встретив его, она побежала снова ко второму велосипедисту.
Так она бегала со скоростью $18$ км/ч от одного велосипедиста к другому, пока велосипедисты не встретились.
Сколько километров пробежала собака?

Ответ: км.

Задание 3:

На станции метро есть два одинаковых эскалатора. Один едет вниз, из здания станции к платформе, а другой - вверх, с платформы в здание станции. Скорость их движения одинакова.

Если мальчик побежит вверх по эскалатору, который едет вниз, он поднимется в здание станции за $2$ минуты.

Если мальчик побежит вверх по поднимающемуся эскалатору, он поднимется в здание станции за $40$ секунд.

За сколько времени мальчик поднимется с платформы в здание, если побежит по остановленному эскалатору?

Ответ: за секунд.

Задание 4:

Почему облака не падают на землю?

Выберите вариант ответа:

Облака всегда легче воздуха, поэтому они не падают на землю.Облака состоят из очень мелких капелек воды, которые падают на землю очень медленно, из-за трения о воздух. Обычно облака образуются в тех местах, где есть восходящий поток тёплого воздуха, и это движение воздуха вверх не даёт образовавшимся мелким капелькам воды упасть. Однако, когда капельки начинают сливаться в более крупные, они начинают падать, и идёт дождь. Так что облака падают на землю в виде дождя, снега или града.

Задание 5:

Винтовой самолет Ан-140 летит со скоростью $550$ км/ч.

Пропеллер этого самолета делает $1200$ оборотов в минуту.

Сколько метров пролетит самолёт за время одного оборота пропеллера? Ответ округлите до десятых.

Ответ: м

Задание 6:

Девочка зажмурила один глаз и обвела на зеркале фломастером отражение своей головы.

Какого размера получится рисунок на поверхности зеркала?

Выберите вариант ответа:

Такого же размера, как голова девочкиВ два раза меньше головы девочкиМы ничего не можем сказать о размере рисунка, возможны разные варианты

Вы можете попробовать проделать этот эксперимент сами.

Конечно, не нужно рисовать на зеркале, но можно приклеить по кусочку клейкой ленты на отражение каждого уха...

Задание 7:

Во время солнечного затмения

Луна находится между Солнцем и Землёй

Земля находится между Солнцем и Луной

на Землю падает тень от Луны

на Солнце падает тень от Земли

38 серия (май) учебного года 2024-2025

За год мы познакомились с понятиями силы и энергии, с одним из самых фундаментальных законов физики - законом сохранения энергии, с законами Ньютона, законом Архимеда, с механизмами, в которых используются подвижные и неподвижные блоки. Приобретенные знания помогут вам решить задачи этой серии.

Задание 1:

На велосипед с колесами диаметром $28$ дюймов во время ремонта по ошибке поставили колеса диаметром $26$ дюймов от другого велосипеда.

Колёса отличались только диаметром обода, звездочки на колесах были одинаковые.

Чтобы заехать на крутую горку, на педали нужно будет давить до ремонта.

Задание 2:

Велосипедист проехал $2$ км по ровной горизонтальной дороге.

При этом он совершил работу $12000$ Дж.

Найдите силу, с которой велосипед отталкивается вперед от дороги.

Ответ:

С какой силой велосипедист должен давить на педаль в положении, показанном на рисунке, чтобы велосипед отталкивался от дороги с такой силой?

Ответ:

Считайте, что потерь энергии при передаче движения с педалей на колесо нет.

Задание 3:

У какого маятника скорость груза в нижней точке больше? (Массы маятников одинаковы, массой нити можно пренебречь).

Выберите вариант ответа:

Скорость красного маятника большеСкорость синего маятника большеСкорость маятников в нижней точке одинакова

Что можно сказать о потенциальной энергии красного и синего маятников в высшей точке подъема?

Выберите вариант ответа:

потенциальная энергия красного маятника большепотенциальная энергия синего маятника большепотенциальная энергия маятников одинакова

Задание 4:

Две одинаковые лодки связаны легкой верёвкой и плавают на расстоянии $60$ м одна от другой. На носу каждой лодки стоит мальчик. Масса обоих мальчиков одинакова. Мальчики одновременно начинают тянуть верёвку. На левой лодке мальчик вытягивает верёвку со скоростью $50$ см/с, а на правой - со скоростью $30$ см/с. Какой путь пройдет левая лодка за одну минуту? Дайте ответ в метрах.

Ответ: м.

Указание: массой веревки можно пренебречь.

Задание 5:

Управлять плавучестью рыбам помогает плавательный пузырь. Для того, чтобы всплыть, рыба выделяет газ из крови в плавательный пузырь, так что общий объем рыбы и ее плавучесть увеличивается. Для погружения рыба, наоборот, уменьшает количество воздуха в пузыре. Для этого рыба растворяет воздух в крови или выпускает его через рот.

В аквариуме плавает толстая голодная рыбка. Она держится в толще воды, не работая плавниками, т.е. только за счёт плавучести.

Как изменится уровень воды в аквариуме, если рыбка случайно проглотит камешки, которые лежат на дне аквариума? Проглотив камешки, рыбка продолжает плавать.

Выберите вариант ответа:

Уровень воды в аквариуме не изменитсяУровень воды в аквариуме повыситсяУровень воды в аквариуме понизится

Задание 6:

Есть два рычага, которые могут свободно качаться.
На каждом из них висят два бруска - один объёмом $1$ литр, а второй - объёмом $2$ литра, как показано на рисунке.

Известно, что бруски тонут в воде.

В случае A плечи рычага равны.

В случае B плечо на стороне большего бруска в $2$ раза короче, чем на стороне меньшего.

Бруски полностью погружены в воду, при этом рычаги находятся в равновесии.

Что произойдёт, если рычаги с брусками достать из воды?

Выберите вариант ответа:

Оба рычага останутся в равновесииВ случае A равновесие не нарушится, а в случае B рычаг выйдет из равновесияВ случае A рычаг выйдет из равновесия, а в случае B равновесие не нарушитсяОба рычага выйдут из равновесия

Задание 7:

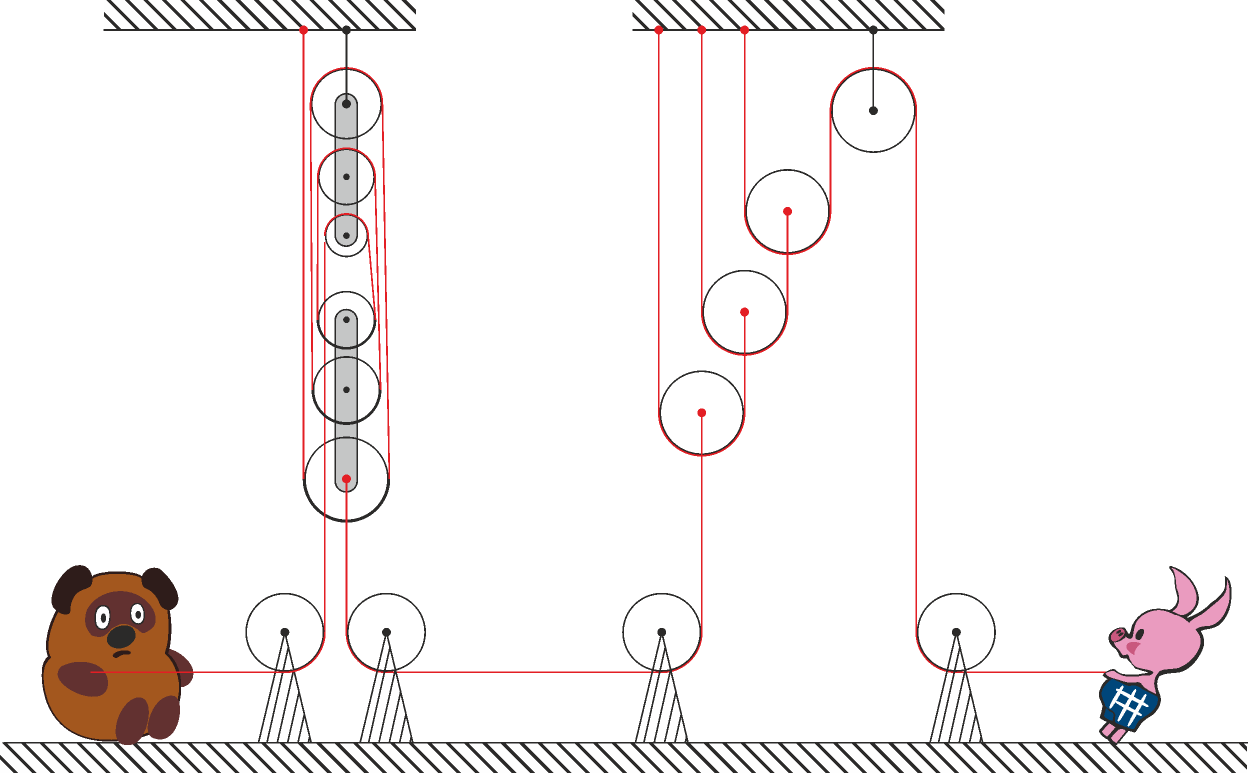
Винни Пух и Пятачок перетягивают канат в устройстве, показанном на рисунке. Оба тянут канат изо всех сил, но никто не может победить. Пятачок тянет канат с силой $30 Н$ . С какой силой тянет канат Винни-Пух?

Дайте ответ в Ньютонах; весом блоков и трением можно пренебречь.

Ответ: $Н$ .

Как записаться в кружок?

Зарегистрироваться в МетаШколе
Войти в МетаШколу со своим логином и паролем
Перейти по ссылке "Все кружки"
Добавить кружок в корзину.
Перейти на страницу "Корзина", выбрать способ оплаты, оплатить.