![Интернет-кружок по математике, 6 класс, примеры [Интернет-кружок по математике, 6 класс, примеры]](/img/theme/subjects/math-64.png) | Интернет-кружок по математике, 6 класс, примерыИнтернет-кружок по математике, 6 класс, примеры |
Примерные серии задач интернет-кружка
Примерные серии задач интернет-кружка
1 серия (сентябрь) учебного года 2025-2026
Теория:
Десятичная система счисления
Натуральные числа - для счёта предметов.
Это числа $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ \dots$
Ряд натуральных чисел бесконечен.
Цифры: $\displaystyle 0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.
Число $\displaystyle 10$ – основание системы счисления.
Счёт идёт десятками, сотнями, тысячами и так далее.
Единица каждого следующего разряда в $\displaystyle 10$ раз больше единицы предыдущего разряда.
Разложение по разрядам:
$\displaystyle 3456 = $ $\displaystyle 3 \cdot 10 \cdot 10 \cdot 10 + 4 \cdot 10 \cdot 10\ + $ $\displaystyle 5 \cdot 10\ + $ $\displaystyle 6 = $ $\displaystyle 3 \cdot 1000 + 4 \cdot 100 + 5 \cdot 10 + 6$.
Признаки делимости:
на $\displaystyle 2$ - натуральное число оканчивается чётной цифрой $\displaystyle 0,\ 2,\ 4,\ 6,\ 8$;
на $\displaystyle 5$ - натуральное число оканчивается цифрой $\displaystyle 0$ или $\displaystyle 5$;
на $\displaystyle 10$ - натуральное число оканчивается цифрой $\displaystyle 0$.
Латинский алфавит ($\displaystyle 26$ букв):
$\displaystyle Aa,\ Bb,\ Cc,\ Dd,\ Ee,\ Ff,\ Gg,$
$\displaystyle Hh,\ Ii,\ Jj,\ Kk,\ Ll,\ Mm,$
$\displaystyle Nn,\ Oo,\ Pp,\ Qq,\ Rr,\ Ss,\ Tt,$
$\displaystyle Uu,\ Vv,\ Ww,\ Xx,\ Yy,\ Zz.$
Учимся решать задачи:
Задание 1:
Найдите наименьшее чётное четырёхзначное число, кратное $\displaystyle 7$ и $\displaystyle 23$.
Задание 2:
Сколько существует натуральных чисел от $\displaystyle 1$ до $\displaystyle 100$, каждое из которых делится на $\displaystyle 5$, но не делится на $\displaystyle 2$, и в своей записи не имеет ни одной тройки?
Задание 3:
В строчку выписаны целые числа от $\displaystyle 1$ до $\displaystyle 1000$. Сколько в этой записи троек?
Задание 4:

Для нумерации страниц книги потребовалось всего $\displaystyle 119$ цифр. Сколько страниц в книге?
Задание 5:
Девять одинаковых блокнотов стоят меньше $\displaystyle 16$ рублей, а тринадцать таких же блокнотов – больше $\displaystyle 23$ рублей. Сколько стоит один блокнот? Дайте ответ в копейках.
Задание 6:
Можно ли рассадить $\displaystyle 46$ кроликов по $\displaystyle 9$ клеткам так, чтобы во всех клетках сидело разное число кроликов и в каждой клетке сидел хотя бы один кролик?
Варианты ответов:
Задание 7:

Четыре белки съели $\displaystyle 1999$ орехов, каждая не меньше, чем $\displaystyle 100$. Первая белка съела больше всех. Вторая и третья вместе съели $\displaystyle 1265$ орехов. Сколько орехов съела первая белка?
Задание 8:
Можно ли из чисел $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$ составить магический квадрат - разместить их в таблице $\displaystyle 3$ на $\displaystyle 3$ так, чтобы суммы чисел по строкам, столбцам и двум диагоналям были одинаковы, и так, чтобы число $\displaystyle 9$ было в угловой клетке?
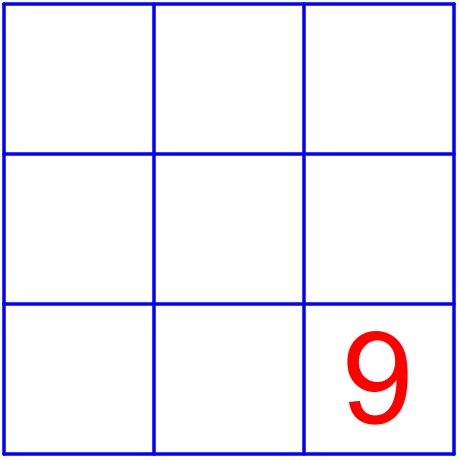
Варианты ответов:
Задание 9:
Можно ли разрезать фигуру по линиям на три равные, совпадающие при наложении, части? Разрезанные фигуры можно переворачивать.
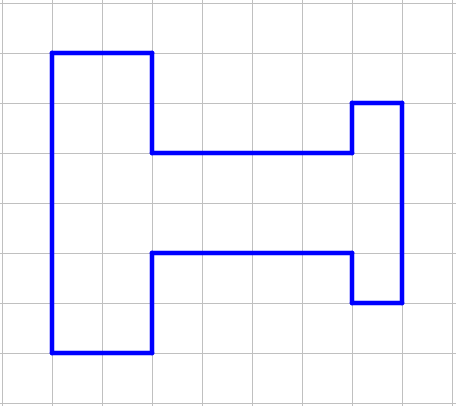
Варианты ответов:
Задание 10:
Сколько кубиков нужно для построения фигуры?

Варианты ответов:
38 серия (май) учебного года 2025-2026
Теория:
Игры
Игры с выигрышными позициями
В таких играх следует искать выигрышную позицию и стремиться передать очередь невыгодного хода противнику.
Задача $\displaystyle 1$
На столе лежат $\displaystyle 34$ камешка. Два игрока по очереди берут $\displaystyle 1$, $\displaystyle 2$ или $\displaystyle 3$ камешка. Проигравшим считается тот, кто возьмёт со стола последние камешки. Кто и как выиграет при правильной игре?
Решение:
Выигрышная стратегия для первого игрока: первому игроку следует первым ходом взять один камешек, а в дальнейшем дополнять число камешков, взятых вторым игроком на последнем ходу, до $\displaystyle 4$.
Ответ: выиграет первый при правильной игре.
Задача $\displaystyle 2$
Игра начинается с числа $\displaystyle 0$. За ход разрешается прибавить к имеющемуся числу любое натуральное число от $\displaystyle 1$ до $\displaystyle 9$. Выиграет тот, кто получит число $\displaystyle 70$. Кто и как выиграет при правильной игре?
Решение:
Выиграет второй. Второй игрок должен прибавлять такое число, чтобы в сумме получить число, делящееся на $\displaystyle 10$.
Ответ: выиграет второй при правильной игре.
Задача $\displaystyle 3$
У ромашки $\displaystyle n$ лепестков. За ход разрешается оторвать либо один лепесток, либо два рядом растущих лепестка. Проигрывает тот, кто не может сделать ход. Кто и как выиграет при правильной игре, если: 1) $\displaystyle n=12$; 2) $\displaystyle n=13$?
Решение:
Выиграет второй игрок в любом случае. Независимо от хода первого игрока, второй может после своего хода оставить две одинаковые по длине цепочки лепестков, а затем делать симметричные ходы.
Ответ: выиграет второй при правильной игре.
Шахматные фигуры
Ход шахматной ладьи

Учимся решать задачи:
Задание 1:
Задание 2:
Задание 3:
Задание 4:
Варианты ответов:
Задание 5:
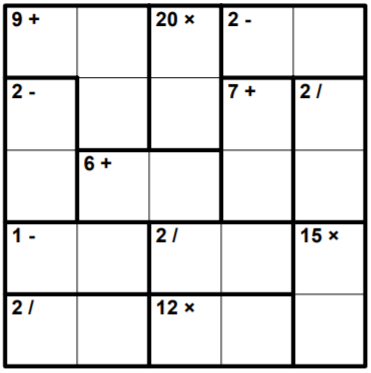
Разгадайте кендоку: заполните клетки числами от $\displaystyle 1$ до $\displaystyle 5$ включительно так, чтобы в каждой строке и в каждом столбце числа не повторялись. Число, которое записано в углу каждого выделенного блока - это результат сложения, вычитания, умножения или деления в этом блоке. Числа внутри блока могут повторяться.
Какое число будет записано в нижней строке в угловой клетке слева?
Задание 6:
Задание 7:

Билет в кино со скидкой в $\displaystyle 20\%$ стоит $\displaystyle 100$ рублей. Сколько стоит билет без скидки? Дайте ответ в рублях.
Задание 8:
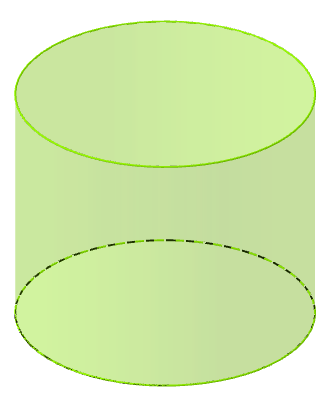
Найдите площадь полной поверхности цилиндра, если радиус его основания равен $\displaystyle 4$ см, а высота равна $\displaystyle 5$ см. Дайте ответ в квадратных сантиметрах с точностью до целых.
Задание 9:
Верно ли утверждение: на картинке можно найти не менее шести пятиугольников?
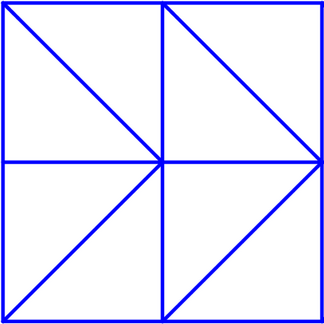
Варианты ответов:
Задание 10:
Можно ли поставить на шахматную доску несколько ладей так, чтобы ровно одна клетка не была бита?

Варианты ответов:
Как записаться в кружок?
- Зарегистрироваться в МетаШколе
- Войти в МетаШколу со своим логином и паролем
- Перейти по ссылке "Все кружки"
- Добавить кружок в корзину.
- Перейти на страницу "Корзина", выбрать способ оплаты, оплатить.
![[Математический кружок]](/img/logo/header-ru-transparent-v5.png)