![Примеры уроков. Летний интенсив по математике — краткое повторение кружка 7 класса [Примеры уроков. Летний интенсив по математике — краткое повторение кружка 7 класса]](/img/theme/subjects/math-64.png) | Примеры уроков. Летний интенсив по математике — краткое повторение кружка 7 классаПримеры уроков. Летний интенсив по математике — краткое повторение кружка 7 класса |
Примеры уроков онлайн-курса «Летний интенсив»
Примеры уроков онлайн-курса «Летний интенсив»
1 урок
Уравнения
Уравнение - это равенство, содержащее неизвестное число, обозначенное буквой.
Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа от знака равенства - правой частью уравнения.
Каждое слагаемое левой и правой части уравнения называется членом уравнения.
Корнем уравнения называется то значение неизвестного, при котором это уравнение обращается в верное равенство.
Модуль числа
Модулем (абсолютной величиной) действительного числа $\displaystyle a$ называется само это число, если оно неотрицательное, и это число, взятое с противоположным знаком, если оно отрицательное.
$\displaystyle \begin{equation*} \lvert a\rvert= \begin{cases} \displaystyle a,& \ a\geqslant0\\ \displaystyle -a,& \ a<0\end{cases} \end{equation*}$
Геометрический смысл модуля: модулем (абсолютной величиной) действительного числа $\displaystyle a$ называется расстояние от точки, изображающей число $\displaystyle a$ на числовой прямой, до точки $\displaystyle 0$.
$\displaystyle |3| = 3$
$\displaystyle |0| = 0$
$\displaystyle |-3| = 3$
Уравнение может иметь один корень.
Например, уравнение $\displaystyle |x-2|=0$ имеет единственный корень: $\displaystyle 2$.
Уравнение может иметь несколько корней.
Например, уравнение $\displaystyle |x|=3$ имеет два корня: $\displaystyle 3;\ -3$.
Уравнение может иметь бесконечно много корней.
Например, уравнение $\displaystyle |x+1|=|x+1|$ имеет бесконечно много корней: любое значение $\displaystyle x$ является корнем этого уравнения.
Уравнение может и не иметь корней.
Например, уравнение $\displaystyle |x|=- 2$ не имеет корней, при любом значении $\displaystyle x$ левая часть этого уравнения больше правой.
Решить уравнение - это значит найти все его корни или установить, что их нет.
Равносильные уравнения
Уравнения, имеющие одно и то же множество корней, называются равносильными.
Уравнения, не имеющие корней, также считаются равносильными.
Например, уравнения $\displaystyle |x|=- 2$ и $\displaystyle |x+5|=-1$ равносильны.
Основные свойства уравнений:
$\displaystyle 1$) Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.
$\displaystyle 2$) Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю.
Решение уравнений с модулем:
$\displaystyle 1)$ Решить уравнение: $\displaystyle |x| = 7$.
Ответ: $\displaystyle 7;\ -7$.
$\displaystyle 2)$ Решить уравнение: $\displaystyle |x| = -5$.
Ответ: решений нет.
$\displaystyle 3)$ Решить уравнение: $\displaystyle |x - 1| = 0$.
Ответ: $\displaystyle 1$.
$\displaystyle 4)$ Решить уравнение: $\displaystyle |2x-1|=3$.
Решение: уравнение равносильно совокупности двух уравнений:
$\displaystyle \bigg [ \begin{align} 2x-1&=3\\ 2x-1&=-3 \end{align} $
Корень первого уравнения - число $\displaystyle 2$, а корень второго – число $\displaystyle -1$.
$\displaystyle \bigg [ \begin{align} x&=2\\ x&=-1 \end{align} $
Ответ: $\displaystyle 2;\ -1$.
$\displaystyle 5)$ Решить уравнение: $\displaystyle |3-5x|=-2$.
Ответ: решений нет.
Учимся решать задачи
Задание 1:
Какое двузначное число в $\displaystyle 17$ раз больше числа его единиц?
Задание 2:
Существует ли такое натуральное число, которое при делении на $\displaystyle 4$ даёт остаток $\displaystyle 1$, а при делении на $\displaystyle 8$ даёт остаток $\displaystyle 3$?
Варианты ответов:
Задание 3:
Первое число составляет $\displaystyle 60\%$ второго, второе – $\displaystyle 50\%$ третьего, а третье – $\displaystyle 20\%$ четвёртого. Найдите первое число, если сумма всех четырёх чисел равна $\displaystyle 272$.
Задание 4:
Сколько решений имеет уравнение:
$\displaystyle 1{,}2:0{,}03+|4x|=1{,}5 \cdot 80$?
Задание 5:
Задание 6:
Три велосипедиста одновременно стартовали по круговой дорожке. Первый делает полный круг за $\displaystyle 4$ мин, второй – за $\displaystyle 6$ мин, а третий – за $\displaystyle 8$ мин. Через сколько минут они ещё раз окажутся вместе на старте? Дайте ответ в минутах.
Задание 7:
В пяти ящиках яблок поровну. Если из каждого ящика взять по $\displaystyle 80$ яблок, то во всех ящиках вместе останется столько яблок, сколько раньше было в трёх ящиках. Сколько яблок было первоначально в каждом ящике?
Задание 8:
Задание 9:
Можно ли из чисел $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$ составить магический квадрат - разместить их в таблице $\displaystyle 3$ на $\displaystyle 3$ так, чтобы суммы чисел по строкам, столбцам и двум диагоналям были одинаковы и так, чтобы число $\displaystyle 4$ было в угловой клетке?
Варианты ответов:
Задание 10:
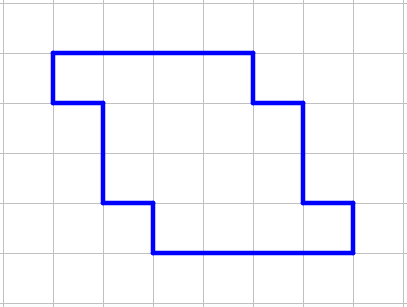
Можно ли разрезать фигуру по линиям на две такие части, из которых складывается квадрат?
Варианты ответов:
20 урок
Модули и параметры
Решение уравнений
$\displaystyle 1)$ Сколько решений имеет уравнение $\displaystyle |x|=a$ в зависимости от $\displaystyle a$?
Решение:
Если $\displaystyle a>0$ - два решения $\displaystyle x=a$ и $\displaystyle x=-a$;
если $\displaystyle a=0$ - одно решение $\displaystyle x=0$;
если $\displaystyle a<0$ - решений нет.
Ответ: если $\displaystyle a>0$ - два; если $\displaystyle a=0$ - одно; если $\displaystyle a<0$ - решений нет.
$\displaystyle 2)$ Сколько решений имеет уравнение $\displaystyle |x-1|=2a$ в зависимости от $\displaystyle a$?
Решение:
Если $\displaystyle a>0$ - два решения $\displaystyle x=2a+1$ и $\displaystyle x=-2a+1$;
если $\displaystyle a=0$ - одно решение $\displaystyle x=1$;
если $\displaystyle a<0$ - решений нет.
Ответ: если $\displaystyle a>0$ - два; если $\displaystyle a=0$ - одно; если $\displaystyle a<0$ - решений нет.
$\displaystyle 3)$ Для каждого значения параметра $\displaystyle a$ определите число корней уравнения $\displaystyle |5x-3|-7=a$.
Решение:
$\displaystyle |5x-3|=a+7$
Если $\displaystyle a=-7$ - одно решение $\displaystyle x=\frac {3}{5}$;
если $\displaystyle a>-7$ - два решения $\displaystyle x=\frac {a+10}{5}$ и $\displaystyle x=\frac {-a-4}{5}$;
если $\displaystyle a<-7$ - решений нет.
Ответ: если $\displaystyle a=-7$ - одно решение; если $\displaystyle a>-7$ - два решения; если $\displaystyle a<-7$ - решений нет.
Учимся решать задачи
Кендоку
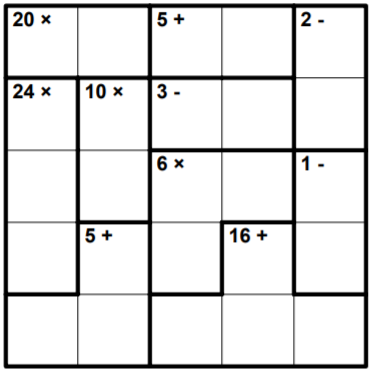
Разгадайте кендоку: заполните клетки числами от $\displaystyle 1$ до $\displaystyle 5$ включительно так, чтобы в каждой строке и в каждом столбце числа не повторялись. Число, которое записано в углу каждого выделенного блока - это результат сложения, вычитания, умножения или деления в этом блоке. Числа внутри блока могут повторяться.
Решение:

Задание 1:
Сколько решений имеет уравнение $\displaystyle |x+3|=5a$ в зависимости от $\displaystyle a$?
Варианты ответов:
Задание 2:
Варианты ответов:
Задание 3:
Задание 4:
Задание 5:
Варианты ответов:
Задание 6:
Решите систему уравнений:
$\displaystyle \begin{cases} \displaystyle 2x+y+z=8\\ \displaystyle x+2y+z=9\\ \displaystyle x+y+2z=11 \end{cases}$
Назовите значение $\displaystyle z$.
Задание 7:
Сколько решений имеет система уравнений?
$\displaystyle \begin{cases} \displaystyle 8x=2(y+1),\\ \displaystyle 4x-y=1 \end{cases}$
Варианты ответов:
Задание 8:
Задание 9:
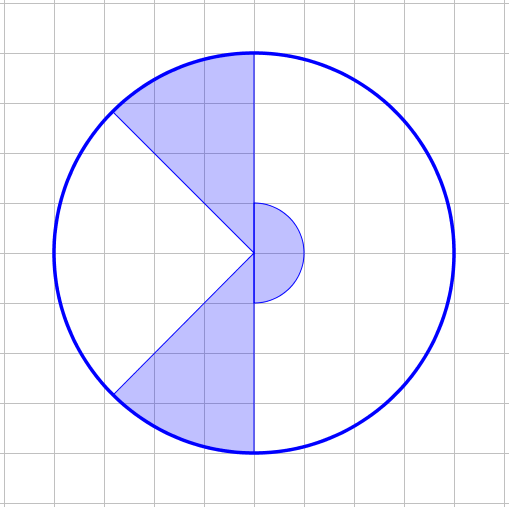
Какая часть фигуры закрашена?
Варианты ответов:
Задание 10:

Разгадайте кендоку: заполните клетки числами от $\displaystyle 1$ до $\displaystyle 5$ включительно так, чтобы в каждой строке и в каждом столбце числа не повторялись. Число, которое записано в углу каждого выделенного блока - это результат сложения, вычитания, умножения или деления в этом блоке. Числа внутри блока могут повторяться.
Какое число будет записано в нижней строке в угловой клетке справа?
![[Математический кружок]](/img/logo/header-ru-transparent-v5.png)