![Примеры уроков. Летний интенсив по математике — краткое повторение кружка 6 класса [Примеры уроков. Летний интенсив по математике — краткое повторение кружка 6 класса]](/img/theme/subjects/math-64.png) | Примеры уроков. Летний интенсив по математике — краткое повторение кружка 6 классаПримеры уроков. Летний интенсив по математике — краткое повторение кружка 6 класса |
Примеры уроков онлайн-курса «Летний интенсив»
Примеры уроков онлайн-курса «Летний интенсив»
1 урок
Теория:
Десятичная система счисления
Натуральные числа - для счёта предметов.
Это числа $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ \dots$
Ряд натуральных чисел бесконечен.
Цифры: $\displaystyle 0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.
Число $\displaystyle 10$ – основание системы счисления.
Счёт идёт десятками, сотнями, тысячами и так далее.
Единица каждого следующего разряда в $\displaystyle 10$ раз больше единицы предыдущего разряда.
Разложение по разрядам:
$\displaystyle 3456 = 3 \cdot 10 \cdot 10 \cdot 10 + 4 \cdot 10 \cdot 10 + $ $\displaystyle 5 \cdot 10 + $ $\displaystyle 6 = $ $\displaystyle 3 \cdot 1000 + 4 \cdot 100 + 5 \cdot 10 + 6$.
Признаки делимости:
на $\displaystyle 2$ - натуральное число оканчивается чётной цифрой $\displaystyle 0,\ 2,\ 4,\ 6,\ 8$;
на $\displaystyle 5$ - натуральное число оканчивается цифрой $\displaystyle 0$ или $\displaystyle 5$;
на $\displaystyle 10$ - натуральное число оканчивается цифрой $\displaystyle 0$.
на $\displaystyle 9$ - сумма цифр числа делится на $\displaystyle 9$;
на $\displaystyle 3$ - сумма цифр числа делится на $\displaystyle 3$;
на $\displaystyle 4$ - две последние цифры числа образуют двузначное число, делящееся на $\displaystyle 4$; например, число $\displaystyle 7924$ делится на $\displaystyle 4$, так как число $\displaystyle 24$ делится на $\displaystyle 4$;
на $\displaystyle 8$ - три последние цифры числа образуют трёхзначное число, делящееся на $\displaystyle 8$; например, число $\displaystyle 79168$ делится на $\displaystyle 8$, так как число $\displaystyle 168$ делится на $\displaystyle 8$.
Двоичная система счисления
В двоичной системе счисления только две цифры $\displaystyle 0$ и $\displaystyle 1$.
С их помощью можно записать любое число.
Счёт ведётся двойками. За основание системы счисления принимается число $\displaystyle 2$.
Число $\displaystyle 2$ записывается в виде $\displaystyle 10_2$, читается "один-нуль".
Каждая единица следующего разряда в $\displaystyle 2$ раза больше предыдущей.
Числа от $\displaystyle 1$ до $\displaystyle 10$ записываются так:
$\displaystyle 1_2$, $\displaystyle 10_2$, $\displaystyle 11_2$, $\displaystyle 100_2$, $\displaystyle 101_2$, $\displaystyle 110_2$, $\displaystyle 111_2$, $\displaystyle 1000_2$, $\displaystyle 1001_2$, $\displaystyle 1010_2$.
Для каждой позиционной системы счисления можно сформулировать свои признаки делимости на то или иное число.
Латинский алфавит ($\displaystyle 26$ букв):
$\displaystyle A,\ B,\ C,\ D,\ E,\ F,\ G,\ H,\ I,\ J,$
$\displaystyle K,\ L,\ M,\ N,\ O,\ P,\ Q,\ R,\ S,\ T,$
$\displaystyle U,\ V,\ W,\ X,\ Y,\ Z. $
Учимся решать задачи
Задание 1:
Найдите наименьшее чётное четырёхзначное число, кратное $\displaystyle 5$ и $\displaystyle 31$.
Задание 2:
В строчку выписаны целые числа от $\displaystyle 1$ до $\displaystyle 1000$. Сколько в этой записи пятёрок?
Задание 3:
Для нумерации страниц книги потребовалось всего $\displaystyle 151$ цифра. Сколько страниц в книге?
Задание 4:
Существует ли такое натуральное число, которое при делении на $\displaystyle 4$ даёт остаток $\displaystyle 2$, а при делении на $\displaystyle 6$ даёт остаток $\displaystyle 3$?
Варианты ответов:
Задание 5:
Варианты ответов:
Задание 6:
Варианты ответов:
Задание 7:
Вставьте пропущенные цифры так, чтобы четырёхзначное число $\displaystyle 67**$ делилось и на $\displaystyle 2$, и на $\displaystyle 3$, и на $\displaystyle 45$. Назовите полученное четырёхзначное число.
Задание 8:
Задание 9:
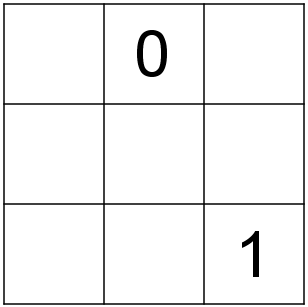
Задание 10:

Сколько кубиков нужно для построения фигуры?
20 урок
Теория:
Игры
Игры с выигрышными позициями
В таких играх следует искать выигрышную позицию и стремиться передать очередь невыгодного хода противнику.
Задача $\displaystyle 1$
Из кучки камней двое играющих по очереди берут $\displaystyle 1$, $\displaystyle 2$ или $\displaystyle 3$ камня. Проигрывает тот, кто берёт последний камень. Как играть второму, чтобы выиграть, если в кучке $\displaystyle 17$ камней?
Решение:
Остаток от деления $\displaystyle 17$ на $\displaystyle 4$ равен $\displaystyle 1$. Выигрышная стратегия для второго игрока: второй должен брать всегда столько, чтобы вместе со своим противником взять $\displaystyle 4$ камня.
Ответ: выиграет второй при правильной игре.
Задача $\displaystyle 2$
У ромашки $\displaystyle n$ лепестков. За ход разрешается оторвать либо один лепесток, либо два рядом растущих лепестка. Проигрывает тот, кто не может сделать ход. Кто и как выиграет при правильной игре, если: 1) $\displaystyle n=12$; 2) $\displaystyle n=13$?
Решение:
Выиграет второй игрок в любом случае. Независимо от хода первого игрока, второй может после своего хода оставить две одинаковые по длине цепочки лепестков, а затем делать симметричные ходы.
Ответ: выиграет второй при правильной игре.
Учимся решать задачи
Кендоку
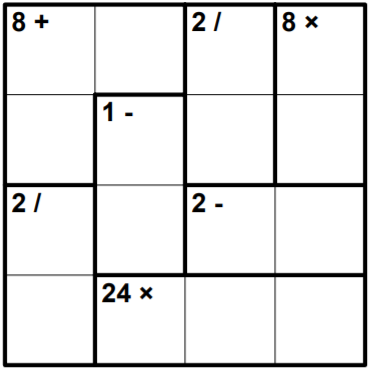
Разгадайте кендоку: заполните клетки числами от $\displaystyle 1$ до $\displaystyle 4$ включительно так, чтобы в каждой строке и в каждом столбце числа не повторялись. Число, которое записано в углу каждого выделенного блока - это результат сложения, вычитания, умножения или деления в этом блоке. Числа внутри блока могут повторяться.
Решение:

Задание 1:
Из кучки в $\displaystyle 20$ камней двое играющих по очереди берут $\displaystyle 1$, $\displaystyle 2$ или $\displaystyle 3$ камня. Проигрывает тот, кто берёт последний камень. Верно ли утверждение: при правильной игре выиграет первый игрок?
Варианты ответов:
Задание 2:
Задание 3:
Задание 4:
Задание 5:
Варианты ответов:
Задание 6:
Задание 7:
В ящике $\displaystyle 20$ белых шаров, $\displaystyle 15$ чёрных и $\displaystyle 10$ красных. На ощупь шары неотличимы друг от друга. Шары вынимают из ящика в темноте. Какое наименьшее число шаров нужно взять, чтобы среди них обязательно оказалось по $\displaystyle 3$ шара каждого цвета?
Задание 8:
Варианты ответов:
Задание 9:
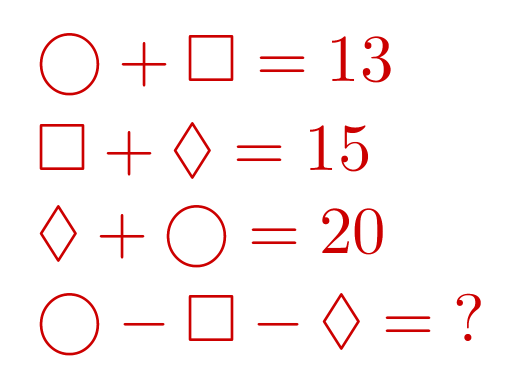
Какое число надо записать вместо вопросительного знака?
Варианты ответов:
Задание 10:
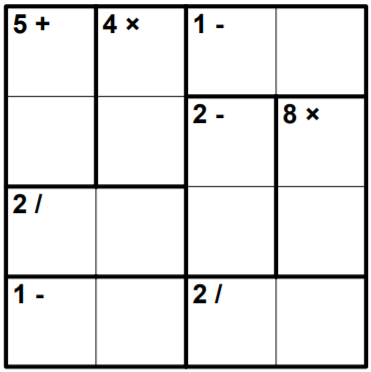
Разгадайте кендоку: заполните клетки числами от $\displaystyle 1$ до $\displaystyle 4$ включительно так, чтобы в каждой строке и в каждом столбце числа не повторялись. Число, которое записано в углу каждого выделенного блока - это результат сложения, вычитания, умножения или деления в этом блоке. Числа внутри блока могут повторяться. Какое число будет записано в верхней строке в угловой клетке справа?
![[Математический кружок]](/img/logo/header-ru-transparent-v5.png)