![Примеры уроков. Летний интенсив по математике — краткое повторение кружка 4 класса [Примеры уроков. Летний интенсив по математике — краткое повторение кружка 4 класса]](/img/theme/subjects/math-64.png) | Примеры уроков. Летний интенсив по математике — краткое повторение кружка 4 классаПримеры уроков. Летний интенсив по математике — краткое повторение кружка 4 класса |
Примеры уроков онлайн-курса «Летний интенсив»
Примеры уроков онлайн-курса «Летний интенсив»
1 урок
Теория:
Десятичная система счисления
Цифры: $\displaystyle 0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.
Натуральные числа - для счёта предметов.
Это числа $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ \dots$
Ряд натуральных чисел бесконечен.
Однозначные натуральные числа: $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.
Двузначные натуральные числа: $\displaystyle 10,\ 11,\ 12,\ 13,\ 14,\ 15,\ ..., 99$.
Трёхзначные натуральные числа: $\displaystyle 100,\ 101,\ 102,\ 103,..., 999$.
Четырёхзначные натуральные числа: $\displaystyle 1000,\ 1001,\ 1002,\ 1003,..., 9999$.
Счёт идёт десятками, сотнями, тысячами и так далее.
$\displaystyle 1$ десяток $\displaystyle = 10$ единиц
$\displaystyle 1$ сотня $\displaystyle = 10$ десятков
$\displaystyle 1$ тысяча $\displaystyle = 10$ сотен
Число $\displaystyle 10$ – основание системы счисления.
Единица каждого следующего разряда (справа налево) в $\displaystyle 10$ раз больше единицы предыдущего разряда.
Разложение по разрядам:
$\displaystyle 2345 = 2 \cdot 1000 + 3 \cdot 100 + 4 \cdot 10 + 5$ (две тысячи, три сотни, четыре десятка и пять единиц).
Цифры в записи числа не повторяются, например: $\displaystyle 1357$.
Цифры в записи числа повторяются, например: $\displaystyle 3183$, $\displaystyle 2922$ или $\displaystyle 7777$.
В числе $\displaystyle 35$ цифра десятков - $\displaystyle 3$, а цифра единиц - $\displaystyle 5$. Цифра единиц на $\displaystyle 2$ больше, чем цифра десятков.
Двоичная система счисления
В двоичной системе счисления только две цифры $\displaystyle 0$ и $\displaystyle 1$.
С их помощью можно записать любое число.
Счёт ведётся двойками. За основание системы счисления принимается число $\displaystyle 2$.
Число $\displaystyle 2$ записывается в виде $\displaystyle 10_2$, читается "один-нуль".
Каждая единица следующего разряда в $\displaystyle 2$ раза больше предыдущей.
Числа от $\displaystyle 1$ до $\displaystyle 10$ записываются так:
$\displaystyle 1_2$, $\displaystyle 10_2$, $\displaystyle 11_2$, $\displaystyle 100_2$, $\displaystyle 101_2$, $\displaystyle 110_2$, $\displaystyle 111_2$, $\displaystyle 1000_2$, $\displaystyle 1001_2$, $\displaystyle 1010_2$.
Русский алфавит ($\displaystyle 33$ буквы): А, Б, В, Г, Д, Е, Ё, Ж, З, И, Й, К, Л, М, Н, О, П, Р, С, Т, У, Ф, Х, Ц, Ч, Ш, Щ, Ъ, Ы, Ь, Э, Ю, Я.
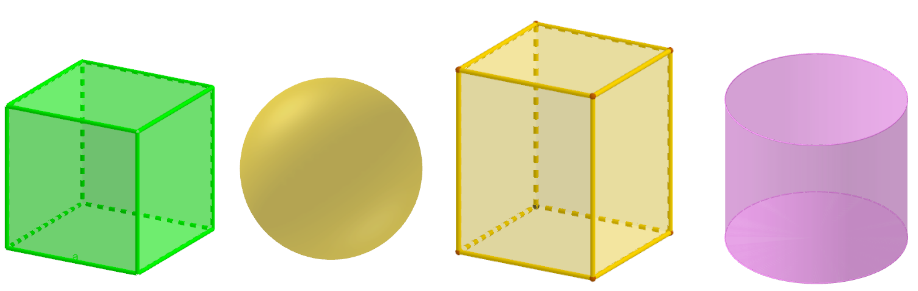
Объёмные фигуры - куб, шар, прямоугольный параллелепипед, цилиндр.
Плоские фигуры - квадрат, круг, треугольник, прямоугольник.

Учимся решать задачи
Задание 1:
Напишите наименьшее число, составленное из пяти различных цифр: $\displaystyle 6,\ 1,\ 0,\ 9,\ 3$.
Задание 2:
Напишите число, состоящее из $\displaystyle 16$ сотен и $\displaystyle 16$ десятков.
Задание 3:
Сколько различных трёхзначных чисел можно составить из цифр $\displaystyle 2,\ 4,\ 8$, если цифры в записи числа могут повторяться?
Задание 4:
Сколько различных четырёхзначных чисел можно составить из двух шестёрок и двух семёрок?
Задание 5:
Какие $\displaystyle 4$ цифры надо вычеркнуть в числе $\displaystyle 52917386$, чтобы оставшиеся цифры в том же порядке составили наименьшее число.
Варианты ответов:
Задание 6:
Как записывается число $\displaystyle 10111_2$ в десятичной системе счисления?
Задание 7:
Во время прогулки по лесу Ваня через каждые $\displaystyle 12$ м находил гриб. Какой путь он проделал от первого гриба до последнего, если всего он нашёл $\displaystyle 6$ грибов? Дайте ответ в метрах.
Задание 8:
Было $\displaystyle 7$ листов бумаги. Некоторые из них разрезали на три части. Всего стало $\displaystyle 15$ листов. Сколько листов бумаги разрезали?
Задание 9:
Задание 10:
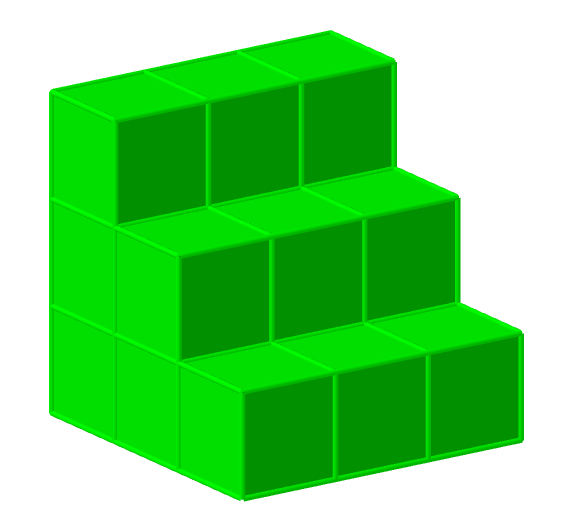
Сколько кубиков нужно для построения фигуры?
20 урок
Теория:
Принцип Дирихле
Задача $\displaystyle 1$

В ящике $\displaystyle 5$ белых шаров, $\displaystyle 6$ чёрных и $\displaystyle 7$ красных. На ощупь шары неотличимы друг от друга. Шары вынимают из ящика в темноте. Какое наименьшее число шаров нужно взять, чтобы среди них обязательно оказалось $\displaystyle 3$ шара разного цвета?
Решение:
В наихудшем случае сначала будут взяты все шары красного и чёрного цвета, следующий шар будет белым.
$\displaystyle 7 + 6+1 = 14$ шаров.
Ответ: $\displaystyle 14$ шаров.
Задача $\displaystyle 2$
В ящике $\displaystyle 5$ белых шаров, $\displaystyle 6$ чёрных и $\displaystyle 7$ красных. На ощупь шары неотличимы друг от друга. Шары вынимают из ящика в темноте. Какое наименьшее число шаров нужно взять, чтобы среди них обязательно был $\displaystyle 1$ белый или $\displaystyle 1$ красный?
Решение:
В наихудшем случае сначала будут взяты все шары чёрного цвета, следующий шар будет белым или красным.
$\displaystyle 6+1 = 7$ шаров.
Ответ: $\displaystyle 7$ шаров.
Развёртка куба
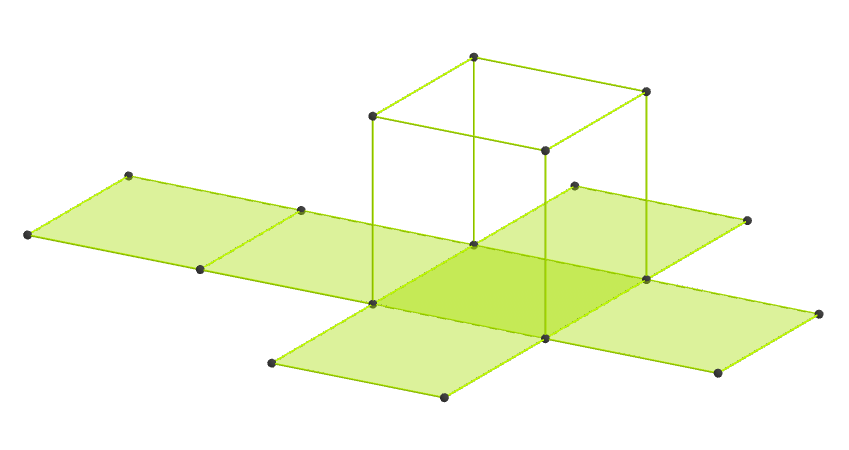
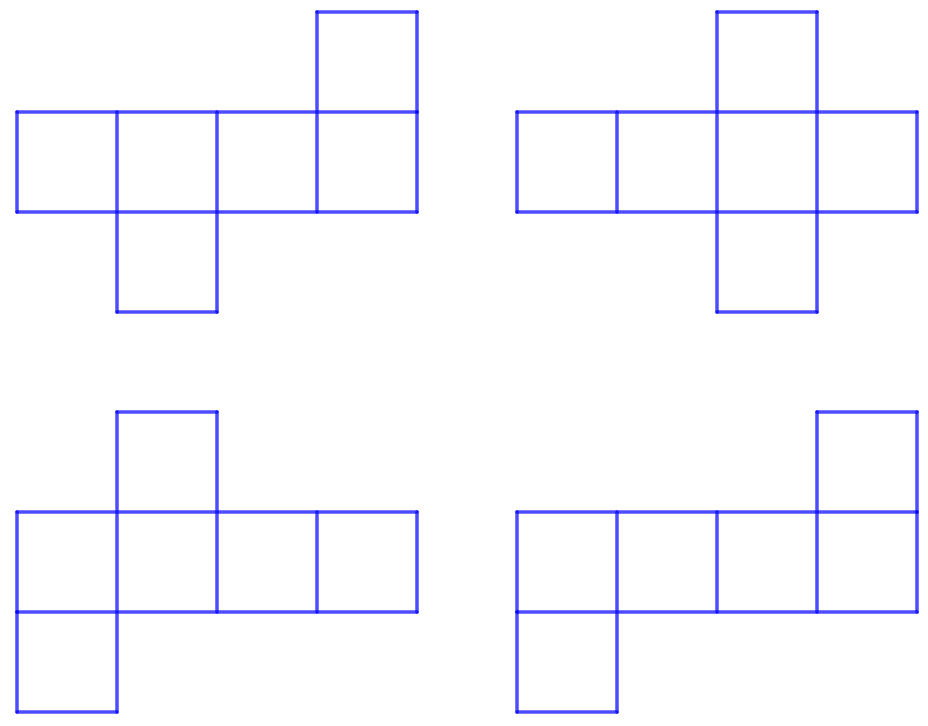
Примеры развёрток куба
Учимся решать задачи
Задание 1:
Задание 2:
Задание 3:
Задание 4:
Варианты ответов:
Задание 5:
Задание 6:
В ящике $\displaystyle 5$ белых шаров, $\displaystyle 10$ чёрных и $\displaystyle 15$ красных. На ощупь шары неотличимы друг от друга. Шары вынимают из ящика в темноте. Какое наименьшее число шаров нужно взять, чтобы среди них обязательно был $\displaystyle 1$ белый или $\displaystyle 1$ чёрный?
Задание 7:
В ящике $\displaystyle 9$ белых шаров, $\displaystyle 10$ чёрных и $\displaystyle 11$ красных. На ощупь шары неотличимы друг от друга. Шары вынимают из ящика в темноте. Какое наименьшее число шаров нужно взять, чтобы среди них обязательно было $\displaystyle 2$ красных или $\displaystyle 2$ чёрных?
Задание 8:
Задание 9:
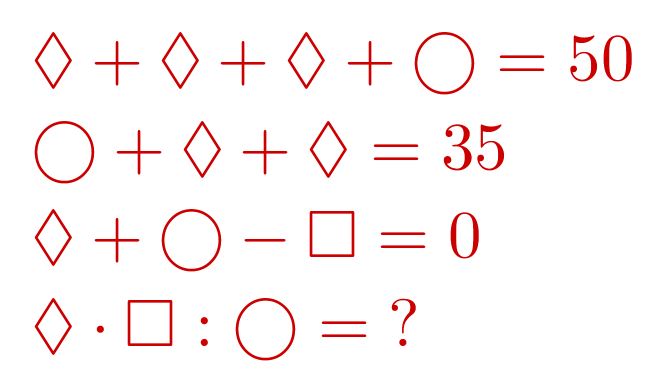
Какое число надо записать вместо вопросительного знака?
Задание 10:
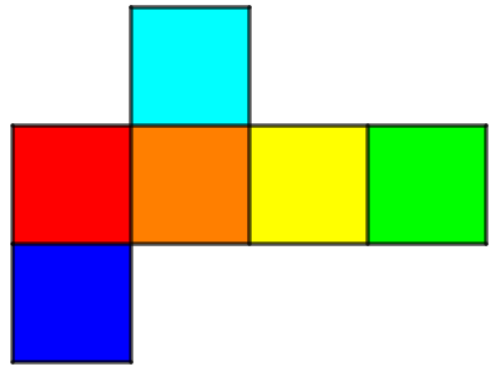
Мысленно сверните куб из развёртки и определите, какая грань является верхней, если нижняя грань голубая?
Варианты ответов:
![[Математический кружок]](/img/logo/header-ru-transparent-v5.png)