![Примеры уроков. Летний интенсив по математике — краткое повторение кружка 1 класса [Примеры уроков. Летний интенсив по математике — краткое повторение кружка 1 класса]](/img/theme/subjects/math-64.png) | Примеры уроков. Летний интенсив по математике — краткое повторение кружка 1 классаПримеры уроков. Летний интенсив по математике — краткое повторение кружка 1 класса |
Примеры уроков онлайн-курса «Летний интенсив»
Примеры уроков онлайн-курса «Летний интенсив»
1 урок
Теория
Цифры: $\displaystyle 0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.
Натуральные числа $\displaystyle -$ для счёта предметов.
Это числа: $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ \dots$
Ряд натуральных чисел бесконечен.
Однозначные натуральные числа:
$\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.
Двузначные натуральные числа:
$\displaystyle 10,\ 11,\ 12,\ 13,\ 14,\ 15,$
$\displaystyle 16,\ 17,\ 18,\ 19,\ 20,\ 21, ..., 99$.
$\displaystyle 1$ десяток $\displaystyle = 10$ единиц
$\displaystyle 1$ сотня $\displaystyle = 10$ десятков
Цифры в записи числа не повторяются, например: $\displaystyle 15$.
Цифры в записи числа повторяются, например: $\displaystyle 33$.
В двузначном числе $\displaystyle 27$ цифра десятков $\displaystyle -$ $\displaystyle 2$, а цифра единиц $\displaystyle -$ $\displaystyle 7$.
Русский алфавит ($\displaystyle 33$ буквы): А, Б, В, Г, Д, Е, Ё, Ж, З, И, Й, К, Л, М, Н, О, П, Р, С, Т, У, Ф, Х, Ц, Ч, Ш, Щ, Ъ, Ы, Ь, Э, Ю, Я.
Объёмные фигуры - куб и шар.

Плоские фигуры - квадрат, круг, треугольник, прямоугольник.

Учимся решать задачи
Задание 1:
Сколько различных двузначных чисел можно составить из цифр $\displaystyle 1,\ 2$ и $\displaystyle 3$, если цифры в записи числа не повторяются?
Задание 2:
Даны цифры: $\displaystyle 3;\ 4$. Сколько различных двузначных чисел можно составить из этих цифр, если цифры в записи числа могут повторяться?
Задание 3:
Сколько существует двузначных чисел, у которых цифра десятков на $\displaystyle 3$ больше, чем цифра единиц?
Задание 4:
Назовите следующее число в ряду:
$\displaystyle 1,\ 2,\ 4,\ 5,\ 7,\ 8,\ 10,\ ... $
Задание 5:
Блокнот дороже тетради, а тетрадь дороже карандаша. Что дешевле - карандаш или блокнот?
Варианты ответов:
Задание 6:
Какие три цифры надо вычеркнуть в числе $\displaystyle 68254$, чтобы оставшиеся цифры в том же порядке составили наибольшее число?
Варианты ответов:
Задание 7:
Найдите закономерность и запишите пропущенную букву: $\displaystyle А,\ Г,\ Ё,\ И,\ \dots,\ О$.
Варианты ответов:
Задание 8:
Сколько надо сделать распилов, чтобы распилить бревно на $\displaystyle 3$ части?
Задание 9:
Задание 10:
Сколько кубиков нужно для построения фигуры?

Варианты ответов:
20 урок
Теория
Принцип Дирихле
Задача $\displaystyle 1$
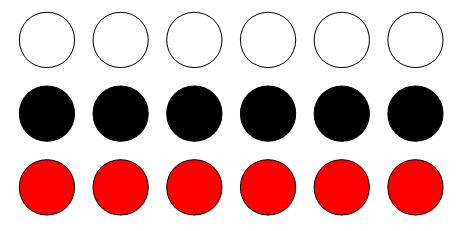
В ящике $\displaystyle 6$ белых шаров, $\displaystyle 6$ чёрных и $\displaystyle 6$ красных. На ощупь шары неотличимы друг от друга. Шары вынимают из ящика в темноте. Какое наименьшее число шаров нужно взять, чтобы среди них обязательно оказалось $\displaystyle 3$ шара разного цвета?
Решение:
В наихудшем случае сначала будут взяты все шары одного и другого цвета, а затем один шар третьего цвета.
$\displaystyle 6+6 + 1 = 13$ шаров.
Ответ: $\displaystyle 13$ шаров.
Задача $\displaystyle 2$
В ящике $\displaystyle 10$ белых шаров, $\displaystyle 10$ чёрных и $\displaystyle 10$ красных. На ощупь шары неотличимы друг от друга. Шары вынимают из ящика в темноте. Какое наименьшее число шаров нужно взять, чтобы среди них обязательно оказалось не менее $\displaystyle 5$ красных?
Решение:
В наихудшем случае сначала будут взяты $\displaystyle 10$ белых и $\displaystyle 10$ чёрных шаров, а затем $\displaystyle 5$ красных.
$\displaystyle 10 + 10 + 5 = 25$ шаров.
Ответ: $\displaystyle 25$ шаров.
Шахматные фигуры
Ход шахматной ладьи

Учимся решать задачи
Задание 1:
Варианты ответов:
Задание 2:
Варианты ответов:
Задание 3:
Задание 4:

Какое число надо написать вместо вопросительного знака?
Задание 5:

У $\displaystyle 5$ велосипедов двухколёсных и трёхколёсных всего $\displaystyle 13$ колёс. Сколько трёхколёсных велосипедов?
Задание 6:
Задание 7:
Задание 8:
Задание 9:
Двое по очереди ставят ладей на шахматную доску размером $\displaystyle 5$ на $\displaystyle 5$ так, чтобы ладьи не били друг друга. Все ладьи одного цвета, каждая ладья бьёт любую другую. Проиграет тот, кто не сможет сделать ход. Кто выиграет?
Варианты ответов:
Задание 10:
Мысленно сверните куб из развёртки и определите, какая грань является верхней, если нижняя грань жёлтая?
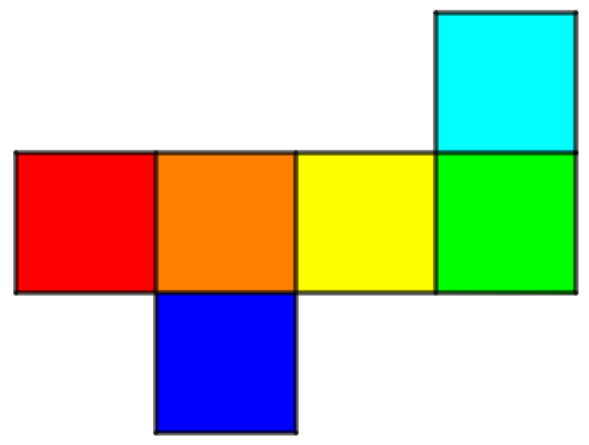
Варианты ответов:
![[Математический кружок]](/img/logo/header-ru-transparent-v5.png)