МетаШкола - Примеры уроков

1 урок

Теория:

Положительные и отрицательные числа

Положительное рациональное число - это число вида $\displaystyle \frac{k}{n}$, где $\displaystyle k$ и $\displaystyle n$ - натуральные числа. Например: $\displaystyle \frac{2}{3}$.

Отрицательное рациональное число - это число вида $\displaystyle - \frac{k}{n}$, где $\displaystyle k$ и $\displaystyle n$ - натуральные числа. Например: $\displaystyle - \frac{6}{7}$.

Рациональными числами называют числа вида $\displaystyle \frac{m}{n}$, где $\displaystyle m$ - целое, $\displaystyle n$ - натуральное.

При возведении отрицательного числа в чётную степень получается положительное число.

При возведении отрицательного числа в нечётную степень получается отрицательное число.

$\displaystyle (-2{,}7)^8>0$

$\displaystyle (-3{,}5)^5<0 $

Учимся решать задачи

Задание 1:

Найдите числовое значение выражения:

$\displaystyle a^3b^4c^9 $

при $\displaystyle a=-3$, $\displaystyle b=-2$, $\displaystyle c=-1$.

Варианты ответов:

432216-72-432144

Задание 2:

Пусть $\displaystyle a<0,\ b>0$.

Выясните, положительно или отрицательно значение выражения: $\displaystyle (3a - 4b)(5b - 2a)(b - a)$?

Варианты ответов:

положительноотрицательно

Задание 3:

Пусть $\displaystyle a<0$. Выясните, положительно или отрицательно число $\displaystyle b$, если $\displaystyle 3ab=-5$?

Варианты ответов:

положительноотрицательно

Задание 4:

Решите уравнение: $\displaystyle (2x-5)(3x+1)=0$.

Варианты ответов:

$\displaystyle - 2{,}5;\ - \frac{1}{3}$$\displaystyle - \frac{1}{3}$$\displaystyle 2{,}5;\ - \frac{1}{3}$$\displaystyle 2{,}5$$\displaystyle 2{,}5;\ \frac{1}{3}$

Задание 5:

Решите уравнение:

$\displaystyle \frac {x^2-9}{x-4}=0.$

Варианты ответов:

$\displaystyle 3;\ -3$$\displaystyle 9;\ 4$$\displaystyle 3;\ -3;\ 4$$\displaystyle 3;\ 4$$\displaystyle 3;\ -3;\ 9$

Задание 6:

Решите уравнение:

$\displaystyle \frac {x^2+2x}{x^2-4}=0.$

Варианты ответов:

$\displaystyle 0;\ -2$корней нет$\displaystyle 0;\ -2;\ 2$$\displaystyle 0$$\displaystyle 0;\ 2$

Задание 7:

Решите уравнение:

$\displaystyle \frac {1}{x-1} - \frac {2}{x^2-1} = 0.$

Варианты ответов:

$\displaystyle -1$$\displaystyle 1$корней нет$\displaystyle 2$$\displaystyle 1;\ -1$

36 урок

Теория:

Метод интервалов

Для решения квадратного неравенства с помощью метода интервалов нужно:

$\displaystyle 1)$ отметить на числовой оси корни уравнения $\displaystyle ax^2+bx+c=0$;

$\displaystyle 2)$ корни разбивают числовую ось на три интервала;

$\displaystyle 3)$ на интервале справа значения трёхчлена $\displaystyle ax^2+bx+c$ положительны при $\displaystyle a > 0$; расставить знаки на остальных интервалах в порядке чередования.

Задача

Решить методом интервалов неравенство: $\displaystyle (x+1)(x-2) > 0$.

Решение:

Отметить на числовой прямой корни уравнения $\displaystyle (x+1)(x-2)=0$ - это точки $\displaystyle -1$ и $\displaystyle 2$.

Эти точки разбивают прямую на три интервала.

На интервале $\displaystyle x > 2$ значения положительны $\displaystyle (x+1)(x-2) > 0$.

Расставить знаки на остальных интервалах в порядке чередования.

$\displaystyle (x+1)(x-2) > 0$ при $\displaystyle x < -1$ и $\displaystyle x > 2$.

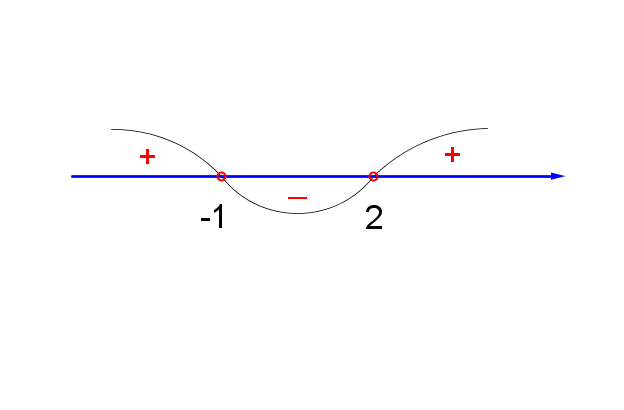
Ответ: $\displaystyle x < -1;\ x > 2$.

Учимся решать задачи

Задание 1:

Решите методом интервалов неравенство: $\displaystyle (x+3)(x-4) > 0$.

Варианты ответов:

$\displaystyle x < -3;\ x > 4$$\displaystyle x > 4$$\displaystyle x < -3$$\displaystyle -3 < x < 4$$\displaystyle -4 < x < 3$

Задание 2:

Решите методом интервалов неравенство: $\displaystyle (x-2)(x+5) < 0$.

Варианты ответов:

$\displaystyle x < 2$$\displaystyle -5 < x < 2$$\displaystyle x < -5;\ x > 2$$\displaystyle x > -5$$\displaystyle -2 < x < 5$

Задание 3:

Решите методом интервалов неравенство: $\displaystyle x^2-7x > 0$.

Варианты ответов:

$\displaystyle -7 < x < 0$$\displaystyle x < 0;\ x > 7$$\displaystyle x > 7$$\displaystyle x < 0$$\displaystyle 0 < x < 7$

Задание 4:

Решите методом интервалов неравенство: $\displaystyle (x^2-1)(x+6) < 0$.

Варианты ответов:

$\displaystyle x < -6;\ -1 < x < 1$$\displaystyle -1 < x < 6$$\displaystyle -6 < x < 1$$\displaystyle -1 < x < 1$$\displaystyle x < -6$

Задание 5:

Решите методом интервалов неравенство: $\displaystyle x^3-9x \geqslant 0$.

Варианты ответов:

$\displaystyle -3 \leqslant x \leqslant 3$$\displaystyle -3 < x < 0$$\displaystyle x \geqslant 3$$\displaystyle -3 < x < 0;\ x > 3$$\displaystyle -3 \leqslant x \leqslant 0;\ x \geqslant 3$

Задание 6:

Решите методом интервалов неравенство: $\displaystyle (x-5)(x+2)(x^2-4) \leqslant 0$.

Варианты ответов:

$\displaystyle -5 \leqslant x \leqslant 2$$\displaystyle -2 \leqslant x \leqslant 5$$\displaystyle -5 \leqslant x \leqslant -2$$\displaystyle x=-2;\ x \geqslant 5$$\displaystyle x=-2;\ 2 \leqslant x \leqslant 5$

Задание 7:

Решите методом интервалов неравенство: $\displaystyle \frac {x^2-3x-4}{x^2+x-6} \geqslant 0$.

Варианты ответов:

$\displaystyle x \leqslant -3;\ -1\leqslant x \leqslant 2;\ x \geqslant 4$$\displaystyle \ -1\leqslant x < 2;\ x \geqslant 4$$\displaystyle x < -3;\ -1\leqslant x < 2;\ x \geqslant 4$$\displaystyle x < -3;\ -1\leqslant x < 2$$\displaystyle -3\leqslant x \leqslant 2;\ x \geqslant 4$

Примеры уроков. Алгебра 8 класс

Примеры уроков. Алгебра 8 класс

Примеры уроков онлайн-курса по школьной программе

Примеры уроков онлайн-курса по школьной программе

1 урок

36 урок