МетаШкола - Примеры уроков - Математика 5 класс

1 урок

Теория:

Натуральные числа:

$\displaystyle 1, \ 2, \ 3, \ 4, \ 5,$

$\displaystyle 6, \ 7, \ 8, \ 9, 10, 11, ...$

Натуральные числа используются для счёта предметов.

Цифры: $\displaystyle 0, \ 1, \ 2, \ 3, \ 4, \ 5, \ 6, \ 7, \ 8, \ 9$.

Чётные цифры: $\displaystyle 0, \ 2, \ 4, \ 6, \ 8$.

Нечётные цифры: $\displaystyle 1, \ 3, \ 5, \ 7, \ 9$.

Десятичная позиционная система счисления

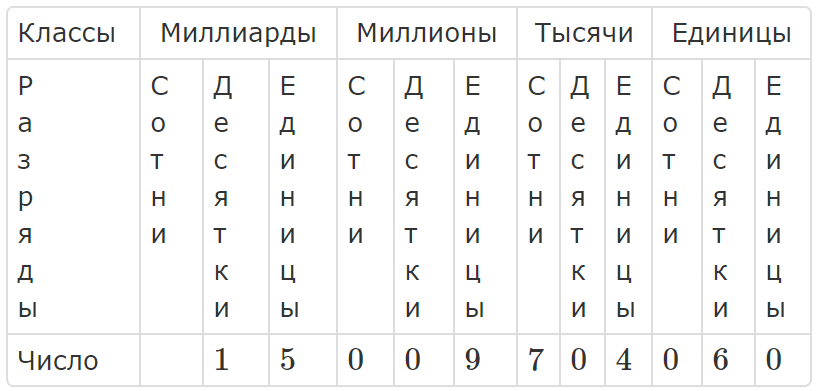
В таблице записано число $\displaystyle 15$ миллиардов $\displaystyle 9$ миллионов $\displaystyle 704$ тысячи $\displaystyle 60$.

Учимся решать задачи

Задание 1:

Запишите цифрами число: двести пять миллиардов восемь тысяч один.

Варианты ответов:

$\displaystyle 205000008001$$\displaystyle 250000800001$$\displaystyle 20508001$$\displaystyle 20500008001$$\displaystyle 205008001$

Задание 2:

Какое натуральное число следует за числом $\displaystyle 29799$?

Варианты ответов:

$\displaystyle 29798$$\displaystyle 29801$$\displaystyle 30800$$\displaystyle 29800$$\displaystyle 30799$

Задание 3:

Сколько тысяч составляют $\displaystyle 2$ миллиона?

Варианты ответов:

$\displaystyle 20$$\displaystyle 200000$$\displaystyle 200$$\displaystyle 20000$$\displaystyle 2000$

Задание 4:

Напишите наибольшее шестизначное число.

Варианты ответов:

$\displaystyle 9999999$$\displaystyle 999999$$\displaystyle 987654$$\displaystyle 900000$$\displaystyle 199999$

Задание 5:

Сколько всего пятизначных чисел, первая цифра которых $\displaystyle 4$?

Варианты ответов:

$\displaystyle 100000$$\displaystyle 90000$$\displaystyle 10000$$\displaystyle 5040$$\displaystyle 50000$

Задание 6:

Напишите наименьшее число, составленное из пяти различных цифр: $\displaystyle 4$, $\displaystyle 2$, $\displaystyle 0$, $\displaystyle 8$, $\displaystyle 6$.

Варианты ответов:

$\displaystyle 02468$$\displaystyle 86420$$\displaystyle 20864$$\displaystyle 24680$$\displaystyle 20468$

Задание 7:

Сколько различных трёхзначных чисел можно составить из цифр $\displaystyle 3$, $\displaystyle 6$ и $\displaystyle 9$? Цифры в записи числа могут повторяться.

Варианты ответов:

$\displaystyle 27$$\displaystyle 3$$\displaystyle 9$$\displaystyle 6$$\displaystyle 15$

43 урок

Теория:

Круговая диаграмма - наглядное изображение путём разбиения круга на части.

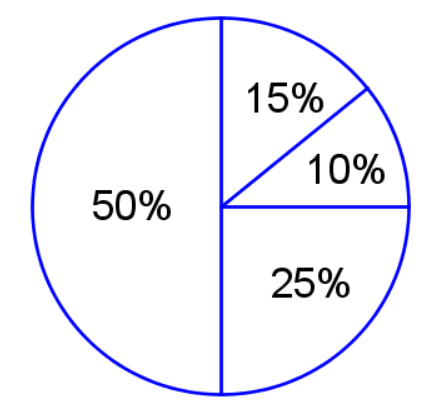
Учимся решать задачи

Задание 1:

Напишите числа в порядке возрастания: $\displaystyle 0,\!6$; $\displaystyle \frac{1}{4}$; $\displaystyle \frac{1}{30}$; $\displaystyle \frac{1}{2}$; $\displaystyle 0,\!53$.

Назовите наибольшее число.

Варианты ответов:

$\displaystyle 0,\!53$$\displaystyle \frac{1}{2}$$\displaystyle 0,\!6$$\displaystyle \frac{1}{4}$$\displaystyle \frac{1}{30}$

Задание 2:

Вычислите: $\displaystyle 8 - (4,\!6 + \frac{17}{100})$.

Варианты ответов:

$\displaystyle 3,\!43$$\displaystyle 3,\!23$$\displaystyle 3,\!57$$\displaystyle 3,\!63$$\displaystyle 3,\!37$

Задание 3:

Периметр прямоугольника $\displaystyle 32,\!9$ см. Длина больше ширины в $\displaystyle 2,\!5$ раза. Найдите площадь прямоугольника.

Варианты ответов:

$\displaystyle 55,\!225$ кв. см$\displaystyle 55,\!2$ кв. см$\displaystyle 52$ кв. см$\displaystyle 55$ кв. см$\displaystyle 55,\!25$ кв. см

Задание 4:

Решите уравнение: $\displaystyle 6,\!2x - 4,\!6 + 2,\!9x = 12 - 0,\!22$.

Варианты ответов:

$\displaystyle 16$$\displaystyle 1,\!8$$\displaystyle 1,\!4$$\displaystyle 1,\!6$$\displaystyle 18$

Задание 5:

Молоко даёт $\displaystyle 25 \%$ сливок, сливки дают $\displaystyle 18 \%$ масла. Сколько масла получится из $\displaystyle 200$ кг молока?

Варианты ответов:

$\displaystyle 8$ кг$\displaystyle 18$ кг$\displaystyle 15$ кг$\displaystyle 9$ кг$\displaystyle 6$ кг

Задание 6:

Собственная скорость лодки $\displaystyle 8$ км/ч, а скорость течения реки $\displaystyle 2,\!6$ км/ч. Какой путь прошла лодка за $\displaystyle 0,\!5$ ч по течению и $\displaystyle 1,\!3$ ч против течения?

Варианты ответов:

$\displaystyle 12,\!32$ км$\displaystyle 16,\!2$ км$\displaystyle 16,\!48$ км$\displaystyle 12,\!3$ км$\displaystyle 12,\!5$ км

Задание 7:

Вычислите: $\displaystyle 0,\!4^{2} \cdot 3,\!5 + (109,\!62 : 2,\!7 - $ $\displaystyle 1,\!6 \cdot 5^{2})^{3} : 0,\!001$.

Варианты ответов:

$\displaystyle 22,\!16$$\displaystyle 360,\!56$$\displaystyle 180,\!56$$\displaystyle 216,\!56$$\displaystyle 0,\!776$

Примеры уроков. Математика 5 класс

Примеры уроков. Математика 5 класс

Примеры уроков онлайн-курса по школьной программе

Примеры уроков онлайн-курса по школьной программе

1 урок

43 урок