Примеры уроков. Математика 6 класс (углублённый уровень)

Десятичная система счисления

Цифры: $\displaystyle 0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.

Натуральные числа — для счёта предметов.

Это числа $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ \dots$

Ряд натуральных чисел бесконечен.

Однозначные натуральные числа: $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.

Двузначные натуральные числа: $\displaystyle 10,\ 11,\ 12,\ 13,\ ..., 99$.

Трёхзначные натуральные числа: $\displaystyle 100,\ 101,\ 102,\ 103,\ ..., 999$.

Четырёхзначные натуральные числа: $\displaystyle 1000,\ 1001,\ 1002,\ 1003,\ ..., 9999$.

$\displaystyle 9$ однозначных натуральных чисел.

$\displaystyle 90$ двузначных натуральных чисел.

$\displaystyle 900$ трёхзначных натуральных чисел.

$\displaystyle 9000$ четырёхзначных натуральных чисел и так далее.

Для записи всех однозначных натуральных чисел потребуется $\displaystyle 9$ цифр.

Для записи всех двузначных натуральных чисел: $\displaystyle 90 \cdot 2=180$ цифр.

Для записи всех трёхзначных натуральных чисел: $\displaystyle 900 \cdot 3=2700$ и так далее.

Число $\displaystyle 10$ — основание системы счисления.

Счёт идёт десятками, сотнями, тысячами и так далее.

Единица каждого следующего разряда (справа налево) в $\displaystyle 10$ раз больше единицы предыдущего разряда.

Задача $\displaystyle 1$

Запишите наименьшее чётное натуральное число, составленное из шести различных цифр.

Решение.

Чётное число оканчивается на чётную цифру. Чётные цифры: $\displaystyle 0,\ 2,\ 4,\ 6,\ 8$.

Шестизначное число не может начинаться с нуля.

Первая цифра — $\displaystyle 1$, вторая — $\displaystyle 0$, остальные цифры в порядке возрастания.

Последняя цифра — чётная цифра $\displaystyle 6$.

Это число: $\displaystyle 102346$.

Ответ: $\displaystyle 102346$.

Задача $\displaystyle 2$

Сколько нечётных натуральных чисел между числами $\displaystyle 100$ и $\displaystyle 500$?

Решение.

Нечётное число оканчивается на нечётную цифру. Нечётные цифры: $\displaystyle 1,\ 3,\ 5,\ 7,\ 9$.

Натуральные числа между числами $\displaystyle 100$ и $\displaystyle 500$: $\displaystyle 101,\ 102,\ 103,\ …,\ 499$.

Это числа от $\displaystyle 101$ до $\displaystyle 499$ включительно.

Чтобы узнать, сколько таких чисел, надо из наибольшего из них вычесть первые $\displaystyle 100$ чисел:

$\displaystyle 499 - 100 = 399$.

Ряд чисел от $\displaystyle 101$ до $\displaystyle 499$ включительно начинается и заканчивается нечётным числом, значит, нечётных чисел больше, чем чётных, на $\displaystyle 1$.

$\displaystyle 399 : 2 = 199$ (ост. $\displaystyle 1$). Чётных — $\displaystyle 199$, нечётных — $\displaystyle 200$.

Ответ: $\displaystyle 200$.

Задача $\displaystyle 3$

Записаны одно за другим подряд все чётные числа натурального ряда $\displaystyle 2468101214161820 …$ Какая цифра будет написана на $\displaystyle 120$-м месте?

Решение.

Первые $\displaystyle 4$ места занимают однозначные чётные числа $\displaystyle 2,\ 4,\ 6,\ 8$.

Чётных двузначных чисел — $\displaystyle 45$, каждое из них записывается двумя цифрами. Для записи всех чётных двузначных потребуется $\displaystyle 90$ цифр.

$\displaystyle 120 - 4 - 90 = 26$ — столько мест занимают чётные трёхзначные числа.

$\displaystyle 26 : 3 = 8$ (ост. $\displaystyle 2$);

$\displaystyle 8$ чётных трёхзначных чисел будут записаны полностью, $\displaystyle 9$-е — только первыми двумя цифрами.

$\displaystyle 100,\ 102,\ 104,\ 106,\ 108,\ 110,\ 112,\ 114,\ 116$.

Вторая цифра числа $\displaystyle 116$ — это цифра $\displaystyle 1$.

Ответ: $\displaystyle 1$.

Задача $\displaystyle 4$

Найдите двузначное число, первая цифра которого равна разности между этим числом и числом, записанным теми же цифрами, но в обратном порядке.

Решение.

Пусть это двузначное число $\displaystyle AB$, где $\displaystyle A$ — цифра десятков, $\displaystyle B$ — цифра единиц.

По условию: $\displaystyle A = AB - BA$.

$\displaystyle A = 10 · A + B - 10 · B - A$;

$\displaystyle A = 9 · A - 9 · B$;

$\displaystyle 9 · B = 8 · A$;

$\displaystyle A = 9;\ B = 8$.

Это число $\displaystyle 98$.

Ответ: $\displaystyle 98$.

Задача $\displaystyle 5$

Цифру $\displaystyle 5$, с которой начиналось четырёхзначное число, перенесли в конец числа. В результате получилось число, которое на $\displaystyle 2925$ меньше. Какое число было первоначально?

Решение.

Пусть первоначальное число $\displaystyle 5ABC$, где $\displaystyle A$ — цифра сотен, $\displaystyle B$ — цифра десятков, $\displaystyle C$ — цифра единиц.

После переноса получилось число $\displaystyle ABC5$.

$\displaystyle 5ABC - ABC5 = 2925$;

$\displaystyle C = 0;\ B = 3;\ A = 2$;

$\displaystyle 5230 - 2305 = 2925$.

Первоначально было число $\displaystyle 5230$.

Ответ: $\displaystyle 5230$.

Импликация высказываний

Импликация — это новое высказывание, образованное из данных высказываний А и В при помощи слов "если …, то …".

Например: "Если данное число делится на $\displaystyle 2$ и на $\displaystyle 3$, то оно делится на $\displaystyle 6$.

Высказывание А называют условием, а высказывание В — заключением.

В рассмотренном примере условием является высказывание "данное число делится на $\displaystyle 2$ и на $\displaystyle 3$", заключением — "число делится на $\displaystyle 6$".

Импликация считается ложным высказыванием только в том случае, когда условие истинно, а заключение ложно.

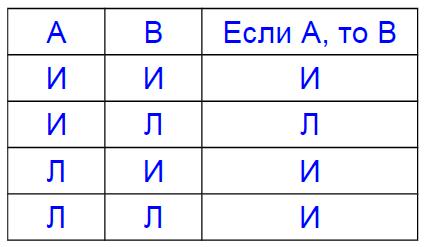
Например:

$\displaystyle 1)$ если число $\displaystyle 12$ делится на $\displaystyle 2$ и на $\displaystyle 3$, то оно делится на $\displaystyle 6$ (истинное высказывание);

$\displaystyle 2)$ если число $\displaystyle 8$ делится на $\displaystyle 2$, то оно делится на $\displaystyle 5$ (ложное высказывание);

$\displaystyle 3)$ если число $\displaystyle 10$ делится на $\displaystyle 3$, то оно делится на $\displaystyle 4$ (истинное высказывание).

Задача $\displaystyle 1$

Какие из данных высказываний истинные:

$\displaystyle 1)$ если $\displaystyle 25$ делится на $\displaystyle 2$, то $\displaystyle 25$ делится на $\displaystyle 3$;

$\displaystyle 2)$ если $\displaystyle 26$ делится на $\displaystyle 13$, то $\displaystyle 26$ делится на $\displaystyle 12$;

$\displaystyle 3)$ если $\displaystyle 27$ делится на $\displaystyle 9$, то $\displaystyle 27$ делится на $\displaystyle 3$;

$\displaystyle 4)$ если $\displaystyle 28$ делится на $\displaystyle 6$, то $\displaystyle 28$ делится на $\displaystyle 7$?

Решение.

Импликация считается ложным высказыванием только в том случае, когда условие истинно, а заключение ложно.

Высказывание $\displaystyle 2$:

условие "$\displaystyle 26$ делится на $\displaystyle 13$" — истинно;

заключение "$\displaystyle 26$ делится на $\displaystyle 12$" — ложно.

Высказывание $\displaystyle 2$ — ложное.

Остальные высказывания $\displaystyle 1,\ 3,\ 4$ — истинные.

Ответ: $\displaystyle 1,\ 3,\ 4$.

Задача $\displaystyle 2$

Определите, кто из трёх девочек играет на скрипке — Аня, Оля или Юля:

$\displaystyle 1)$ играет или Аня, или Оля;

$\displaystyle 2)$ Аня и Юля — обе играют или обе не играют;

$\displaystyle 3)$ если играет Аня, то играет Оля?

Решение.

Все три высказывания будут истинными, если играет Оля.

Высказывание $\displaystyle 1$ — Аня не играет, Оля играет.

Высказывание $\displaystyle 2$ — Аня и Юля — обе не играют.

Высказывание $\displaystyle 3$ — импликация:

условие "если играет Аня" — ложно, значит, высказывание $\displaystyle 3$ — истинное.

Ответ: Оля.

Задача $\displaystyle 3$

А, В и С - жители острова рыцарей и лжецов. Рыцари всегда говорят правду, а лжецы всегда лгут.

А говорит: "Мы все лжецы".

В говорит: "Один из нас рыцарь".

Кто из них рыцарь и кто лжец?

Решение.

Рассмотреть все возможные варианты для A, B и C:

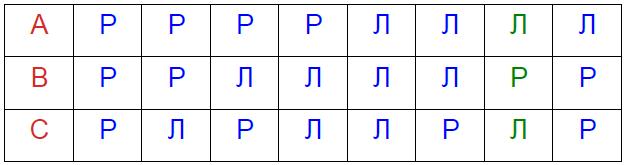
А — не рыцарь, рыцарь не мог сказать "Мы все лжецы", А — лжец.

Тогда В — рыцарь, С лжец.

Ответ: А и С — лжецы, В — рыцарь.

Задача $\displaystyle 4$

Три подруги были в белом, жёлтом и красном платьях. Их туфли были тех же цветов. Только у Иры цвета платья и туфель совпадали. Маша была в белых туфлях. Ни платье, ни туфли Даши не были жёлтыми. Определите цвет платья и туфель у Иры.

Решение.

Маша была в белых туфлях.

У Даши туфли не жёлтые и не белые, тогда туфли красные.

Платье у Даши не жёлтое и не красное, тогда платье белое.

Жёлтое платье и жёлтые туфли у Иры.

Ответ: жёлтые туфли, жёлтое платье.

Задача $\displaystyle 5$

В коробке лежат белые и красные шарики, всего $\displaystyle 12$ шариков. Известно, что среди любых $\displaystyle 8$ из них имеется хотя бы один белый шарик, а среди любых $\displaystyle 6$ — хотя бы один красный шарик. Сколько белых и сколько красных шариков в коробке?

Решение.

Среди любых $\displaystyle 8$ из них имеется хотя бы один белый шарик, тогда красных не может быть больше, чем $\displaystyle 8 - 1 = 7$.

Среди любых $\displaystyle 6$ — хотя бы один красный шарик, тогда белых шариков не может быть больше, чем $\displaystyle 6 - 1 = 5$.

В коробке $\displaystyle 5$ белых и $\displaystyle 7$ красных шариков.

Варианты ответов:

Варианты ответов:

Варианты ответов:

Варианты ответов: