Примеры уроков. Математика 5 класс (углублённый уровень)

Десятичная система счисления

Цифры: $\displaystyle 0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.

Натуральные числа - для счёта предметов.

Это числа $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ \dots$

Ряд натуральных чисел бесконечен.

Однозначные натуральные числа: $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.

Двузначные натуральные числа: $\displaystyle 10,\ 11,\ 12,\ 13,\ ..., 99$.

Трёхзначные натуральные числа: $\displaystyle 100,\ 101,\ 102,\ 103,\ ..., 999$.

Четырёхзначные натуральные числа: $\displaystyle 1000,\ 1001,\ 1002,\ 1003,\ ..., 9999$.

$\displaystyle 9$ однозначных натуральных чисел.

$\displaystyle 90$ двузначных натуральных чисел.

$\displaystyle 900$ трёхзначных натуральных чисел.

$\displaystyle 9000$ четырёхзначных натуральных чисел и так далее.

Для записи всех однозначных натуральных чисел потребуется $\displaystyle 9$ цифр.

Для записи всех двузначных натуральных чисел: $\displaystyle 90 \cdot 2=180$ цифр.

Для записи всех трёхзначных натуральных чисел: $\displaystyle 900 \cdot 3=2700$ и так далее.

Число $\displaystyle 10$ – основание системы счисления.

Счёт идёт десятками, сотнями, тысячами и так далее.

$\displaystyle 1$ десяток $\displaystyle = 10$ единиц

$\displaystyle 1$ сотня $\displaystyle = 10$ десятков

$\displaystyle 1$ тысяча $\displaystyle = 10$ сотен

Единица каждого следующего разряда (справа налево) в $\displaystyle 10$ раз больше единицы предыдущего разряда.

Разложение по разрядам:

$\displaystyle 47258=40000+7000+200+50+8$

$\displaystyle 1003060=1000000+3000+60$

$\displaystyle 2483 = 2 \cdot 1000\ + $ $\displaystyle 4 \cdot 100\ + $ $\displaystyle 8 \cdot 10 + 3$.

Цифры в записи числа не повторяются, например: $\displaystyle 3041$.

Цифры в записи числа повторяются, например: $\displaystyle 2925,\ 3633,\ 5555$.

В числе $\displaystyle 45$ цифра десятков - $\displaystyle 4$, а цифра единиц - $\displaystyle 5$. Цифра единиц на $\displaystyle 1$ больше, чем цифра десятков.

В числе $\displaystyle 28$ сумма цифр числа равна $\displaystyle 2 + 8 = 10$, а произведение цифр этого числа равно $\displaystyle 2 \cdot 8 = 16$.

В числе $\displaystyle 34567$ каждая последующая цифра на единицу больше, чем предыдущая.

Разные логические задачи

Задача $\displaystyle 1$

На острове рыцарей и лжецов разговаривают A и B. Рыцари всегда говорят правду, а лжецы всегда лгут.

A говорит: "По крайней мере один из нас лжец".

Что можно сказать об A и B?

Решение:

Рассмотреть все возможные варианты для A и B:

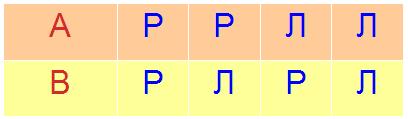
Из этих четырёх вариантов подходит только один:

A — рыцарь, B — лжец.

Ответ: A — рыцарь, B — лжец.

Задача $\displaystyle 2$

A, B и С — жители острова рыцарей и лжецов. Рыцари всегда говорят правду, а лжецы всегда лгут.

A говорит: "Мы все лжецы".

B говорит: "Среди нас два рыцаря".

Кто такой С — рыцарь или лжец?

Решение:

Рассмотреть все возможные варианты для A, B и C:

А — лжец, рыцарь не мог сказать: "Мы все лжецы".

Если В — рыцарь, то С тоже рыцарь.

Если В — лжец, то С — рыцарь.

Если С — лжец, то тогда три лжеца, и получается, что А сказал правду — противоречие.

Ответ: С — рыцарь.

Задача $\displaystyle 3$

В трёх ящиках находятся крупа, вермишель и сахар. На первом ящике написано "крупа", на втором — "вермишель", на третьем — "крупа или сахар". Надписи не соответствуют тому, что находится в ящиках. Что находится в первом ящике?

Решение:

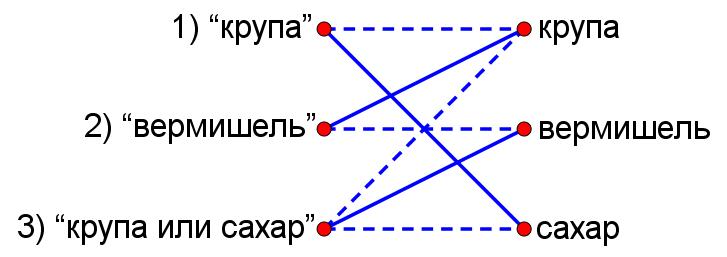
На третьем ящике написано — "крупа или сахар", надпись не соответствует, в третьем ящике вермишель.

Если в первом ящике не крупа и не вермишель, то тогда сахар.

Во втором ящике — крупа.

В первом ящике — сахар, во втором — крупа, в третьем — вермишель.

Ответ: сахар.

Задача $\displaystyle 4$

В забеге участвовали Аня, Оля, Юля. После окончания соревнований две из них дали верные высказывания:

Аня: "Я не была первой".

Оля: "Я не была ни первой, ни третьей".

Какое место заняла Юля?

Решение:

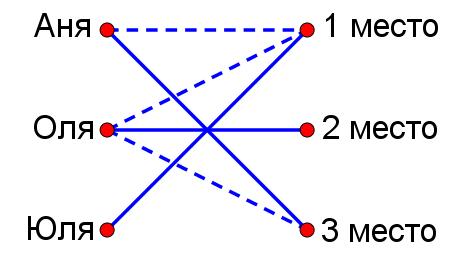
Оля не была ни первой, ни третьей, Оля была второй.

Аня — ни первой, ни второй, Аня была третьей.

Тогда Юля была первой.

Юля — $\displaystyle 1$ место, Оля — $\displaystyle 2$ место, Аня — $\displaystyle 3$ место.

Ответ: $\displaystyle 1$.

Задача $\displaystyle 5$

В чашке, стакане, кувшине и банке находятся молоко, лимонад, квас и вода. Известно, что вода и квас не в чашке; в банке не чай и не квас; вода не в стакане и не в банке. Что в стакане?

Решение:

Если в банке не вода, не чай и не квас, то тогда в банке молоко.

Если вода не в чашке, не в стакане и не в банке, то тогда вода в кувшине.

В чашке — не вода, не квас и не молоко, значит, в чашке — чай, а в стакане — квас.

В чашке — чай, в стакане — квас, в кувшине — вода, в банке — молоко.

Ответ: квас.

Варианты ответов:

Варианты ответов: