Примеры уроков. Математика 4 класс (углублённый уровень)

Десятичная система счисления

Цифры: $\displaystyle 0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.

Натуральные числа — для счёта предметов.

Это числа $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ \dots$

Ряд натуральных чисел бесконечен.

Однозначные натуральные числа: $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.

Двузначные натуральные числа: $\displaystyle 10,\ 11,\ 12,\ 13,\ ..., 99$.

Трёхзначные натуральные числа: $\displaystyle 100,\ 101,\ 102,\ 103,\ ..., 999$.

Четырёхзначные натуральные числа: $\displaystyle 1000,\ 1001,\ 1002,\ 1003,\ ..., 9999$.

Число $\displaystyle 10$ — основание системы счисления.

Счёт идёт десятками, сотнями, тысячами и так далее.

$\displaystyle 1$ десяток $\displaystyle = 10$ единиц

$\displaystyle 1$ сотня $\displaystyle = 10$ десятков

$\displaystyle 1$ тысяча $\displaystyle = 10$ сотен

Единица каждого следующего разряда (справа налево) в $\displaystyle 10$ раз больше единицы предыдущего разряда.

Разложение по разрядам:

$\displaystyle 35617=30000+5000+600+10+7$

$\displaystyle 1002040=1000000+2000+40$

$\displaystyle 2345 = 2 \cdot 1000\ + $ $\displaystyle 3 \cdot 100\ + $ $\displaystyle 4 \cdot 10 + 5$ (две тысячи, три сотни, четыре десятка и пять единиц).

Цифры в записи числа не повторяются, например: $\displaystyle 1357$.

Цифры в записи числа повторяются, например: $\displaystyle 3183,\ 2922,\ 7777$.

В числе $\displaystyle 35$ цифра десятков — $\displaystyle 3$, а цифра единиц — $\displaystyle 5$. Цифра единиц на $\displaystyle 2$ больше, чем цифра десятков.

В числе $\displaystyle 36$ сумма цифр числа равна $\displaystyle 3 + 6 = 9$, а произведение цифр этого числа равно $\displaystyle 3 \cdot 6 = 18$.

В числе $\displaystyle 23456$ каждая последующая цифра на единицу больше, чем предыдущая.

Разные логические задачи

Задача $\displaystyle 1$

В чашке, стакане и банке находятся молоко, квас и вода. Известно, что сосуд с водой стоит рядом с банкой; в чашке не квас и не вода. Что в банке?

Решение:

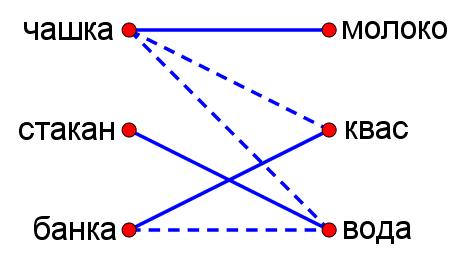
Если в банке не вода, то тогда молоко или квас.

В чашке не квас и не вода, тогда — молоко.

В чашке — молоко, в стакане — вода, в банке — квас.

Ответ: квас.

Задача $\displaystyle 2$

Одна из девочек разбила чашку — Катя, Юля или Оля. На вопрос, кто это сделал, Катя сказала: "Чашку разбила Юля". Оля с Юлей тоже ответили, но так тихо, что никто не услышал. В последствии оказалось, что правду сказала только одна девочка, она и разбила чашку. Кто разбил чашку?

Решение:

Катя сказала: "Чашку разбила Юля".

Правду сказала только одна девочка, она и разбила чашку.

Катя не могла разбить чашку, она солгала, Юля не могла разбить чашку.

Чашку разбила Оля.

Ответ: Оля.

Задача $\displaystyle 3$

В забеге участвовали Ваня, Саша и Олег. После окончания соревнований каждого из них спросили, какое он место занял. Ребята дали верные ответы:

Ваня: "Я не был вторым".

Саша: "Я не был первым".

Олег: "Я был первым".

Кто прибежал третьим?

Решение:

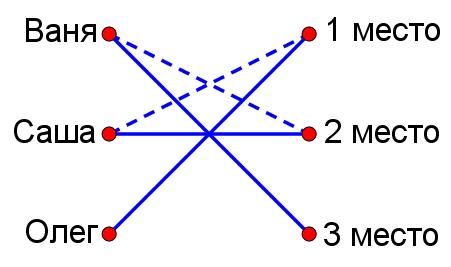
Олег — первый, Саша — второй, Ваня — третий.

Ответ: Ваня.

Задача $\displaystyle 4$

Ваня, Петя и Боря учатся в одной школе. Один ездит домой из школы на автобусе, другой на трамвае, третий на троллейбусе. Однажды после уроков, Ваня пошёл проводить друга до остановки троллейбуса. Когда мимо них проходил автобус, третий друг крикнул из окна автобуса: "Петя, ты забыл в школе тетрадь". Кто на чём ездит домой?

Решение:

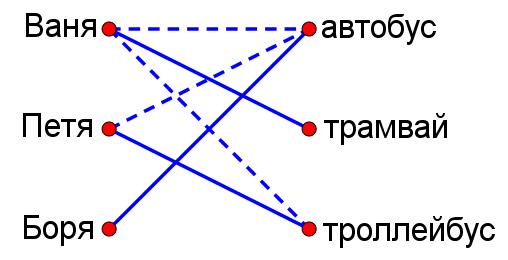
Ответ: Ваня — на трамвае, Петя — на троллейбусе, Боря — на автобусе.

Задача $\displaystyle 5$

Одна из четырёх девочек играет на скрипке — Таня, Аня, Оля или Юля. Кто играет на скрипке, если:

$\displaystyle 1)$ играет или Таня, или Аня, или Юля;

$\displaystyle 2)$ играет или Таня, или Оля, или Юля;

$\displaystyle 3)$ Юля не играет на скрипке?

Решение:

Из первых двух высказываний следует, что играет Таня или Юля.

Третье высказывание "Юля не играет на скрипке", тогда играет Таня.

Ответ: Таня.

Варианты ответов:

Варианты ответов:

Варианты ответов:

Варианты ответов: