Примеры уроков. ОГЭ по математике для 9 класса

Основное свойство дроби

Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.

$\displaystyle \frac{a}{b}=\frac{a \cdot c}{b \cdot c}= \frac{a : c}{b : c}$

Сокращение дробей - деление числителя и знаменателя на их общий делитель, отличный от единицы.

$\displaystyle \frac{15}{20} = \frac{15 : 5}{20 : 5} = \frac{3}{4}$

Деление и дроби

$\displaystyle a:b= \frac{a}{b}$

$\displaystyle 5:6= \frac{5}{6}$

$\displaystyle 6:2= \frac{6}{2}=3$

Любое натуральное число можно записать в виде дроби с любым натуральным знаменателем.

$\displaystyle 3= \frac{3 \cdot 5}{5}=\frac{15}{5}$

Сложение и вычитание дробей с одинаковыми знаменателями

$\displaystyle \frac{a}{c} + \frac{b}{c} = \frac{a+b}{c}$

$\displaystyle \frac{a}{c} - \frac{b}{c} = \frac{a-b}{c}$

Приведение дробей к общему знаменателю

$\displaystyle 1)$ Найти НОК знаменателей (это и есть наименьший общий знаменатель).

$\displaystyle \frac {3}{4}$ и $\displaystyle \frac {5}{6}$; НОК$\displaystyle (4;\ 6) = 12$

$\displaystyle 2)$ Найти для каждой дроби дополнительный множитель (разделить наименьший общий знаменатель на знаменатель дроби).

$\displaystyle 12:4=3$ и $\displaystyle 12:6=2$

$\displaystyle 3)$ Умножить числитель и знаменатель каждой дроби на её дополнительный множитель.

$\displaystyle \frac {3}{4} = \frac {3 \cdot 3}{4 \cdot 3} = \frac {9}{12}$

$\displaystyle \frac {5}{6} = \frac {5 \cdot 2}{6 \cdot 2} = \frac {10}{12}$

Сравнение, сложение и вычитание дробей с разными знаменателями

$\displaystyle 1)$ Привести дроби к наименьшему общему знаменателю $\displaystyle (m)$.

$\displaystyle 2)$ Сравнить

$\displaystyle \frac {a}{m} > \frac {b}{m}$, если $\displaystyle a > b$

Сложить

$\displaystyle \frac {a}{m} + \frac {b}{m} = \frac {a+b}{m}$

Вычесть

$\displaystyle \frac {a}{m} - \frac {b}{m} = \frac {a-b}{m}$

Смешанные числа

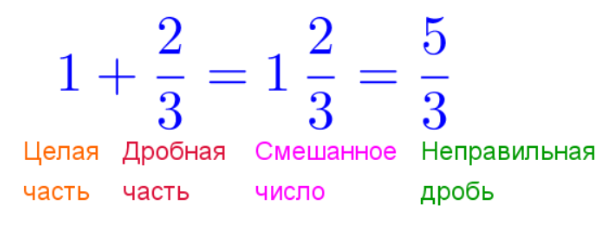
Сложение смешанных чисел

$\displaystyle 1)$ Привести дробные части к наименьшему общему знаменателю.

$\displaystyle 2)$ Сложить отдельно целые и дробные части.

Если при сложении дробных частей получилась неправильная дробь, выделить целую часть и прибавить её к полученной целой части.

$\displaystyle 5\frac{5}{6} + 3\frac{3}{4} = 5\frac{10}{12} + 3\frac{9}{12} = $

$\displaystyle =8\frac{19}{12} = 9\frac{7}{12}$

Вычитание смешанных чисел

$\displaystyle 1)$ Привести дробные части к наименьшему общему знаменателю.

Если дробная часть уменьшаемого меньше дробной части вычитаемого, превратить её в неправильную дробь, уменьшив на единицу целую часть.

$\displaystyle 2)$ Вычесть отдельно целые и дробные части.

$\displaystyle 3\frac{4}{9} - 1\frac{5}{6} = 3\frac{8}{18} - 1\frac{15}{18} =$

$\displaystyle = 2\frac{26}{18} - 1\frac{15}{18} = 1\frac{11}{18}$

Умножение дроби на натуральное число

$\displaystyle \frac{a}{b} \cdot n = \frac{a \cdot n}{b}$

$\displaystyle \frac{3}{4} \cdot 5 = \frac{3 \cdot 5}{4} = \frac{15}{4} = 3\frac{3}{4}$

Умножение дробей

$\displaystyle \frac{a}{b} \cdot \frac{c}{d} = \frac{a \cdot c}{b \cdot d}$

$\displaystyle \frac{3}{8} \cdot \frac{4}{15} = \frac{3 \cdot 4}{8 \cdot 15} = $

$\displaystyle =\frac{1}{2 \cdot 5} = \frac{1}{10}$

Умножение смешанных чисел

Записать в виде неправильных дробей, а затем воспользоваться правилом умножения дробей.

$\displaystyle 9\frac{3}{5} \cdot 1\frac{5}{12} = \frac{48}{5} \cdot \frac{17}{12} =$

$\displaystyle = \frac{48 \cdot 17}{5 \cdot 12} = \frac{4 \cdot 17}{5} =\frac{68}{5} = 13\frac{3}{5}$

Применение распределительного свойства умножения

$\displaystyle 1)$ $\displaystyle \Big(\frac{4}{5} - \frac{1}{3}\Big) \cdot 15 = $

$\displaystyle =\frac{4}{5} \cdot 15 - \frac{1}{3} \cdot 15 = 12-5=7$

$\displaystyle 2)$ $\displaystyle 2\frac{1}{14} \cdot 7 = \Big(2+\frac{1}{14}\Big) \cdot 7 =$

$\displaystyle = 2 \cdot 7+ \frac{1}{14} \cdot 7 = 14 + \frac{1}{2} = 14\frac{1}{2}$

$\displaystyle 3)$ $\displaystyle \frac{3}{8} \cdot a + \frac{1}{4}\cdot a =$

$\displaystyle =\Big( \frac{3}{8} + \frac{1}{4}\Big)\cdot a =\Big( \frac{3}{8} + \frac{2}{8}\Big)\cdot a= \frac{5}{8} \cdot a$

Деление

Чтобы разделить одну дробь на другую, надо делимое умножить на число, обратное делителю.

$\displaystyle \frac{a}{b} : \frac{c}{d} = \frac{a}{b} \cdot \frac{d}{c} = \frac{a \cdot d}{b \cdot c} $

$\displaystyle 2\frac{2}{5} : 1\frac{1}{15} = \frac{12}{5} : \frac{16}{15} =$

$\displaystyle = \frac{12}{5} \cdot \frac{15}{16} = \frac{12 \cdot 15}{5 \cdot 16} = $

$\displaystyle =\frac{3 \cdot 3}{4} = \frac{9}{4} = 2\frac{1}{4}$

Дробные выражения - частное двух чисел или выражений, в котором знак деления обозначен чертой.

Пример.

$\displaystyle \frac{\frac{3}{4}+\frac{7}{8}}{1 \frac{3}{10}-\frac{4}{5}} = \frac{\frac{6}{8}+\frac{7}{8}}{\frac{1}{2}} = \frac{13}{8} : \frac{1}{2}=$

$\displaystyle = \frac{13}{8} \cdot \frac{2}{1} = \frac{13}{4} = 3\frac{1}{4}$

Варианты ответов:

Варианты ответов:

Варианты ответов:

Варианты ответов:

Варианты ответов:

Свойства степени с целым показателем

Если $\displaystyle a \neq 0$ и $\displaystyle n$ — натуральное число, то $\displaystyle a^{-n}=\frac{1}{a^n}$.

Если $\displaystyle n=0$, то $\displaystyle a^0=1$.

Для любых $\displaystyle a \neq 0, \ b \neq 0$ и любых целых $\displaystyle n$ и $\displaystyle m$ справедливы равенства:

$\displaystyle 1. \ a^na^m=a^{n+m}$

$\displaystyle 2. \ a^n:a^m=a^{n-m}$

$\displaystyle 3. \ (a^n)^m=a^{nm}$

$\displaystyle 4. \ (ab)^n=a^nb^n$

$\displaystyle 5. \ \Big(\frac{a}{b}\Big)^n=\frac{a^n}{b^n}$