![Примеры уроков. Физика 7 класс [Примеры уроков. Физика 7 класс]](/img/theme/subjects/physics-64.png) | Примеры уроков. Физика 7 классПримеры уроков. Физика 7 класс |
Примеры уроков онлайн-курса по школьной программе
Примеры уроков онлайн-курса по школьной программе
1 урок
Пример измерения физической величины - как измерить объём тела?
_________________________
Цена деления прибора
Как найти цену деления шкалы прибора?
1. Найти два ближайших штриха шкалы, возле которых написаны значения величин.
2. Вычесть из большего значения меньшее.
3. Полученное число разделить на число делений, находящихся между ними.
Например, цена деления линейки равна $\displaystyle 0{,}1 \ см=1\ мм$ .
![]()
Найдём цену деления мерного цилиндра:
![]()
На шкале этого мерного цилиндра на $\displaystyle 15$ мл приходится $\displaystyle 5$ делений.
Цена деления шкалы равна: $\displaystyle \quad \frac{15\; мл}{5\; делений}=3$ мл.
При считывании показаний нужно обязательно обращать внимание на цену деления прибора.
Например, столбик термометра поднялся на одинаковую высоту:
![]()
А одинаковую ли температуру показывают термометры?
Цена деления шкалы у термометров разная, поэтому показания различны.
Первый термометр показывает плюс $\displaystyle 34$ градуса, а второй - плюс $\displaystyle 17$ градусов.
Задание 1:
При забеге на $\displaystyle 60$ метров на уроке физкультуры засекли время при помощи механического секундомера.
Красная стрелка - секундная, её показания считывают по внешней шкале.
Внутренний маленький круг - для минутной стрелки, при решении этой задачи на него не надо обращать внимания.
Секундомер остановлен в тот момент, когда Петя финишировал.
![]()
1. Какова цена деления секундной шкалы секундомера?
Цена деления секундной шкалы:
2. C какой скоростью бежал Петя?
Дайте ответ в метрах в секунду, с точностью до сотых.
Ответ: м/с.
Задание 2:
Расположите мерные цилиндры в порядке возрастания цены деления.
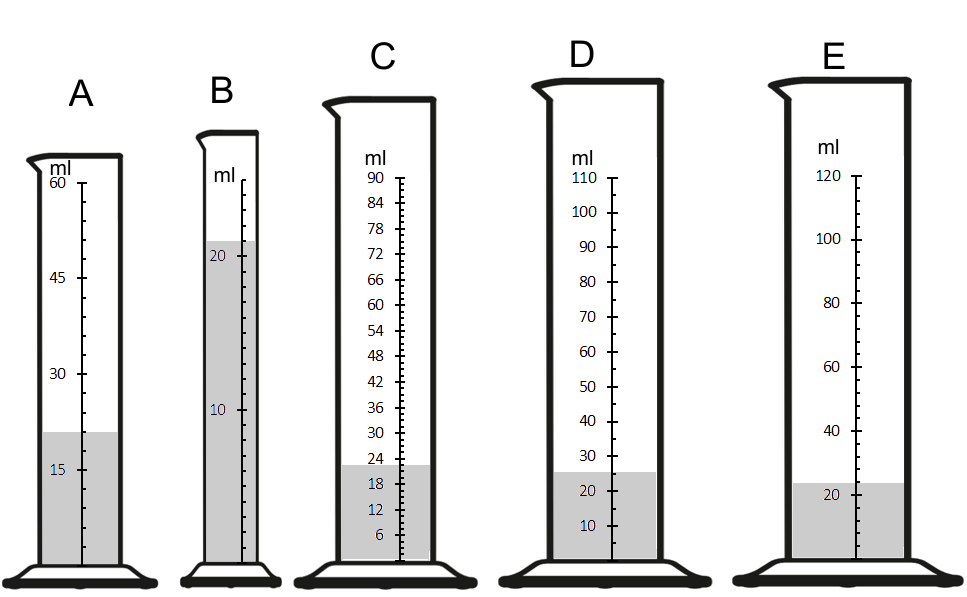
Задание 3:
Для взвешивания соли на чашечных весах есть набор разновесов:
| $\displaystyle 1\ г$ | - | 1 шт. |
| $\displaystyle 2\ г$ | - | 1 шт. |
| $\displaystyle 5\ г$ | - | 1 шт. |
| $\displaystyle 10\ г$ | - | 1 шт. |
| $\displaystyle 20\ г$ | - | 1 шт. |
| $\displaystyle 50\ г$ | - | 1 шт. |
Можно ли отмерить столько соли за одно взвешивание:
Указание: разновесы можно ставить на обе чаши весов.
Фото: Википедия, Poussin jean [CC BY-SA 3.0]
Задание 4:
На рисунке показан мерный цилиндр с водой до и после того, как в него на нитке опустили камень.
Шкала на цилиндре указана в миллилитрах.
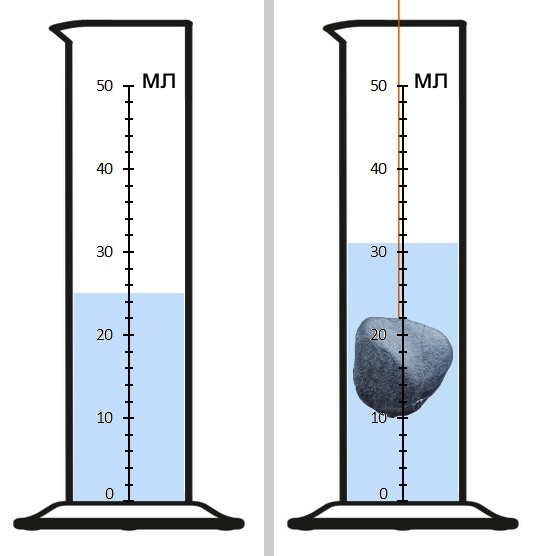
Чему равна цена деления шкалы мерного цилиндра?
Дайте ответ в миллилитрах.
Ответ: мл.
Найдите объем камня. Дайте ответ в миллилитрах.
Ответ: мл .
Задание 5:
Какого роста был Конек-Горбунок?
В сказке "Конек-Горбунок" говорится:
| "Там увидел он красивых Двух коней золотогривых, Еще третьего конька, Ростом только в три вершка На спине с двумя горбами Да с аршинными ушами" |
Аршин и вершок - старинные русские единицы длины.
$\displaystyle 1$ аршин равен $\displaystyle 0{,}7112$ метра.
В одном аршине $\displaystyle 16$ вершков.
Сколько сантиметров в трёх вершках?
Ответ: три вершка - это см.
Задание 6:
Переведите в указанные единицы измерения:
$\displaystyle l=8{,}4$ км = м = см.
$\displaystyle l=135$ см= м = мм.
$\displaystyle t=23$ часа = минут = секунд.
$\displaystyle S=400 \ м^2$ = $\displaystyle дм^2$ = $\displaystyle см^2$.
$\displaystyle V=5{,}8 \ м^3$ = $\displaystyle дм^3$ = $\displaystyle см^3$.
Задание 7:
Какой из автомобильных спидометров показывает большую скорость?
| 1. mph=miles per hour = мили в час $\displaystyle 1\ миля = 1609 \ м$ | 2. km/h = километры в час
|
Ответ:
30 урок
Коэффициент полезного действия
При решении задач про простые механизмы мы всегда рассматривали идеальные устройства, в которых нет трения. Мы не учитывали вес самих блоков и рычагов.
В реальных блоках приходится дополнительно совершать работу по подъёму самого блока, верёвок, и работу по преодолению силы трения в оси блока.
Совершённая с помощью механизма полезная работа всегда немного меньше полной совершённой работы.
Отношение полезной работы к полной работе называется коэффициентом полезного действия механизма.
КПД обычно выражают в процентах и обозначают греческой буквой $\displaystyle \eta$.
$\displaystyle \eta=\frac{A_{полезная}}{A_{полная}}$
Задача.
![]()
При равномерном подъёме груза массой $\displaystyle 2{,}2\ кг$ при помощи блока динамометр показывает $\displaystyle 25\ Н$.
Каков коэффициент полезного действия блока?
Считайте $\displaystyle g=10\ Н/кг$.
Решение.
Раньше при решении задач мы всегда рассматривали идеальные блоки, в которых нет трения.
Если бы блок был идеальным, то для того, чтобы поднять груз массой $\displaystyle 2{,}2$ кг, надо было бы приложить силу $\displaystyle \approx22$ Н.
Но в этой задаче учитывается трение в блоке, и человеку приходится тянуть за верёвку с силой $\displaystyle 25$ Н, потому что приходится преодолевать силу трения.
При подъёме груза на высоту $\displaystyle h$ совершается полезная работа:
$\displaystyle A_{полезная}=P\cdot h=m\cdot g\cdot h$
При этом человек вытягивает кусок веревки длиной $\displaystyle h$, прикладывая силу $\displaystyle F=25\ Н$.
Значит, полная (затраченная) работа равна:
$\displaystyle A_{полная}=F\cdot h$
Коэффициент полезного действия равен:
$\displaystyle \eta=\frac{A_{полезная}}{A_{полная}}\cdot 100\%$
$\displaystyle \eta=\frac{m\cdot g\cdot h}{F\cdot h}\cdot 100\%=\frac{22}{25}\cdot 100\%=88\%$
Пример вычисления КПД. КПД резинового мотора.
Задание 1:
Мальчик катит чемодан на колёсиках вверх по наклонному коридору.
Масса чемодана $\displaystyle 10 \ кг$, мальчик прошел $\displaystyle 50$ метров и при этом поднялся на $\displaystyle 2$ метра. На протяжении всего пути он тянул чемодан с силой $\displaystyle 8 \ Н$.
Каков коэффициент полезного действия колёс чемодана при таком наклоне пола?
Ответ: %.
Считайте $\displaystyle g=10\ Н/кг$
Указание: полезная работа - это работа по подъёму чемодана против силы тяжести.
Задание 2:
![]()
Человек поднимает груз при помощи наклонной плоскости.
У какой наклонной плоскости больше коэффициент полезного действия?
Считайте для простоты, что сила трения груза о наклонную плоскость в обоих случаях одинакова.
Ответ: Коэффициент полезного действия .
Задание 3:
Механик достаёт двигатель из машины при помощи ручной лебёдки.
Чтобы поднять двигатель массой $\displaystyle 150\ кг$ на $\displaystyle 1{,}6\ м$, ему пришлось сделать $\displaystyle 128$ оборотов рукояткой лебедки, постоянно прикладывая к ней силу $\displaystyle 20\ Н$.
Длина рукоятки равна $\displaystyle 20\ см$, это соответствует длине окружности, по которой движется рука механика, равной $\displaystyle 1{,}25 \ м$.
Считайте $\displaystyle g=10\ Н/кг$.
Ответ: КПД составляет %.
Задание 4:
Коэффициент полезного действия гидравлического подъемника равен $\displaystyle 90\%$.
Каковы будут потери энергии при подъеме автомобиля массой $\displaystyle 1250 \ кг$ на высоту $\displaystyle 190\ см$?
Считайте $\displaystyle g=10\ Н/кг$.
Ответ: Потери энергии (бесполезная работа) составят примерно Дж.
Задание 5:
Рабочий поднял груз с пола на некоторую высоту при помощи рычага.
Выяснилось, что рабочий совершил механическую работу на $\displaystyle 25\%$ больше, чем другой рабочий, который поднял груз на ту же высоту без рычага.
Каков был КПД рычага?
Ответ: КПД рычага был %.
С чем могут быть связаны потери энергии при подъеме груза?
Задание 6:
![]()
При помощи одинаковых блоков груз массой $\displaystyle 1$ кг поднимают на одинаковую высоту. Массы самих блоков одинаковы и равны $\displaystyle 200$ г, трение в блоках одинаковое.
Одинаковы ли КПД этих установок?
Ответ:
Указание: полезная работа - это работа по подъёму груза.
Задание 7:
Вентилятор потребляет мощность $\displaystyle 25$ Вт.
При этом он создаёт поток воздуха в $\displaystyle 0{,}1 \ м^3/с$, а скорость воздуха в потоке за вентилятором равна $\displaystyle 10 \ м/с$.
Плотность воздуха равна $\displaystyle 1{,}25 \ кг/м^3$
Каков КПД вентилятора?
Ответ: %.
Указание: Полезная работа затрачивается на то, чтобы привести воздух в движение, то есть на сообщение воздуху кинетической энергии.
![[Математический кружок]](/img/logo/header-ru-transparent-v5.png)