МетаШкола - Примеры уроков

1 урок

Многочлен $\displaystyle n$-степени:

$\displaystyle P_n(x)=a_0x^n+a_1x^{n-1}+ $ $\displaystyle \dots +$ $\displaystyle a_{n-1}x+$ $\displaystyle a_n,$

где $\displaystyle a_0, \ a_1, \ \dots, \ a_{n-1}, \ a_n$ — заданные числа, $\displaystyle a_0 \neq 0$, $\displaystyle n$ — натуральное число.

Деление многочленов нацело:

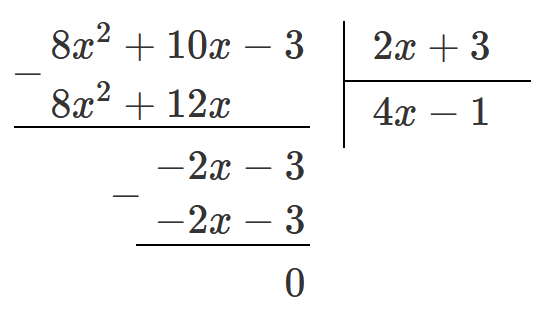
Деление многочленов с остатком:

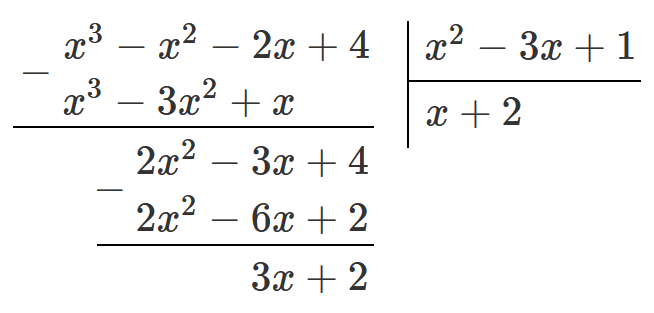
Учимся решать задачи

Задание 1:

Найдите частное: $\displaystyle (x^2-6x+8):(x-2)$.

Варианты ответов:

$\displaystyle x-3$$\displaystyle x-4$$\displaystyle x$$\displaystyle x-1$$\displaystyle x-2$

Задание 2:

Найдите частное: $\displaystyle (2x^3+3x^2-8x+3):(x+3)$.

Варианты ответов:

$\displaystyle 2x^2-x+3$$\displaystyle 2x^2-x+1$$\displaystyle 2x^2-3x+1$$\displaystyle 2x^2-x$$\displaystyle 2x^2-3x+3$

Задание 3:

Выполните деление: $\displaystyle (5x^3+9x^2-17x+3):(x^2+2x-3)$.

Варианты ответов:

$\displaystyle 5x$$\displaystyle 4x+1$$\displaystyle 5x-1$$\displaystyle 4x-1$$\displaystyle 5x+1$

Задание 4:

Найдите остаток от деления многочлена на многочлен: $\displaystyle (4x^3+10x^2- 7x-8):(x+3)$.

Варианты ответов:

$\displaystyle -1$$\displaystyle -3$$\displaystyle -4$$\displaystyle -2$$\displaystyle -5$

Задание 5:

Найдите остаток от деления многочлена на многочлен: $\displaystyle (3x^4- 9x^3+2x^2-10x$ $\displaystyle +18):(3x^3+$ $\displaystyle 2x-$ $\displaystyle 4)$.

Варианты ответов:

$\displaystyle x+6$$\displaystyle -6$$\displaystyle x$$\displaystyle 6$$\displaystyle x-6$

Задание 6:

Делится ли нацело многочлен $\displaystyle P(x)$ на многочлен $\displaystyle Q(x)$?

$\displaystyle P(x)=6x^5-30x^4-3x^3+15x^2-$ $\displaystyle 2x+$ $\displaystyle 11$;

$\displaystyle Q(x)=x-5$.

Варианты ответов:

данет

Задание 7:

При каком значении $\displaystyle k$ многочлен $\displaystyle P(x)$ делится нацело на многочлен $\displaystyle Q(x)?$

$\displaystyle P(x)=3x^6+2x^4+kx^2+1$;

$\displaystyle Q(x)=3x^4+5x^2-1$.

Варианты ответов:

$\displaystyle -5$$\displaystyle -6$$\displaystyle 5$$\displaystyle -1$$\displaystyle 6$

32 урок

Учимся решать задачи

Задание 1:

Решите уравнение: $\displaystyle 2x^3+9x^2+3x-4=0$.

Варианты ответов:

$\displaystyle -1; \ \frac{1}{2}; \ -4$$\displaystyle -1; \ -\frac{1}{2}; \ 4$$\displaystyle 1; \ -2; \ 4$$\displaystyle -1; \ 2; \ -4$$\displaystyle 1; \ 2; \ 4$

Задание 2:

Решите систему уравнений: $\displaystyle \begin{cases} x^2+y^2=52;\\ xy=-24. \end{cases}$

Варианты ответов:

$\displaystyle (-4; \ 6), \; (6; \ -4), \; (-6; \ 4), \; (4; \ -6)$$\displaystyle (-4; \ -6), \; (6; \ 4), \; (-6; \ 4), \; (4; \ -6)$$\displaystyle (-4; \ 6), \; (6; \ -4)$$\displaystyle (-6; \ 4), \; (4; \ -6)$$\displaystyle (-4; \ -6), \; (6; \ 4)$

Задание 3:

Упростите выражение: $\displaystyle 9+5\sqrt{3}\cdot (2-\sqrt{3})^2$.

Варианты ответов:

$\displaystyle 5\sqrt{3}$$\displaystyle \sqrt{3}-1$$\displaystyle 35\sqrt{3}-51$$\displaystyle 19$$\displaystyle -35$

Задание 4:

Найдите область определения функции: $\displaystyle y=\sqrt{x^3-4x}$.

Варианты ответов:

$\displaystyle [-2; \ 0]; \; [2; \ +\infty)$$\displaystyle [-2; \ +\infty)$$\displaystyle (-\infty; \ -2]; \; [0; \ 2]$$\displaystyle [0; \ 2]$$\displaystyle (-\infty; \ -2]$

Задание 5:

Найдите сумму первых десяти членов арифметической прогрессии, если $\displaystyle a_1=5, \; d=-2$.

Варианты ответов:

$\displaystyle -30$$\displaystyle -25$$\displaystyle 50$$\displaystyle 10$$\displaystyle -40$

Задание 6:

Решите уравнение: $\displaystyle \sqrt{x+3}+\sqrt{2x-3}=6$.

Варианты ответов:

$\displaystyle 222$$\displaystyle 6; \ 222$$\displaystyle 36$$\displaystyle 6; \ 36$$\displaystyle 6$

Задание 7:

Построить график функции $\displaystyle y=2-\frac{1}{x^2}$.

Варианты ответов:

Примеры уроков. Алгебра 9 класс

Примеры уроков. Алгебра 9 класс

Примеры уроков онлайн-курса по школьной программе

Примеры уроков онлайн-курса по школьной программе

1 урок

32 урок