![Примеры уроков. Математика 4 класс (базовый уровень) [Примеры уроков. Математика 4 класс (базовый уровень)]](/img/theme/subjects/math-64.png) | Примеры уроков. Математика 4 класс (базовый уровень)Примеры уроков. Математика 4 класс (базовый уровень) |
Примеры уроков онлайн-курса по школьной программе
Примеры уроков онлайн-курса по школьной программе
1 урок
Натуральные числа
$\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9,\ $ $\displaystyle 10,\ $ $\displaystyle 11,\ $ $\displaystyle 12,\ $ $\displaystyle 13,\ $ $\displaystyle 14,\ $ $\displaystyle 15,\ \dots$
Ряд натуральных чисел бесконечен.
Однозначные натуральные числа:
$\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.
Двузначные натуральные числа:
$\displaystyle 10,\ 11,\ 12,\ 13,\ 14,\ 15,\ $ $\displaystyle 16,\ $ $\displaystyle 17,\ $ $\displaystyle 18,\ $ $\displaystyle 19,\ $ $\displaystyle 20,\ $ $\displaystyle 21,\ $ $\displaystyle ...,\ 99$.
Трёхзначные натуральные числа:
$\displaystyle 100,\ 101,\ 102,\ ...,\ 999$.
Цифры:
$\displaystyle 0, \ 1, \ 2, \ 3, \ 4, \ 5, \ 6, \ 7, \ 8, \ 9$.
Чётные цифры: $\displaystyle 0, \ 2, \ 4, \ 6, \ 8$.
Нечётные цифры: $\displaystyle 1, \ 3, \ 5, \ 7, \ 9$.
Задание 1:
Запиши число, которое содержит:
$\displaystyle 5$ сотен $\displaystyle 6$ десятков $\displaystyle 7$ единиц
Ответ:
$\displaystyle 6$ сотен $\displaystyle 0$ десятков $\displaystyle 3$ единицы
Ответ:
$\displaystyle 7$ сотен $\displaystyle 9$ десятков $\displaystyle 0$ единиц
Ответ:
$\displaystyle 8$ сотен $\displaystyle 0$ десятков $\displaystyle 0$ единиц
Ответ:
$\displaystyle 9$ сотен $\displaystyle 9$ десятков $\displaystyle 9$ единиц
Ответ:
Задание 2:
Вычисли:
$\displaystyle 570-150+280=$
$\displaystyle 640+230-770=$
$\displaystyle 780-230-350=$
$\displaystyle 150·6-450=$
$\displaystyle 480:8+540=$
Задание 3:
Назови пропущенное число:
$\displaystyle 490-$ $\displaystyle =800:2$
$\displaystyle 570+$ $\displaystyle =7·100$
$\displaystyle 999+1=600+$
$\displaystyle 85+$ $\displaystyle =700:7$
$\displaystyle 800-$ $\displaystyle =150·4$
Задание 4:
Сравни числа:
$\displaystyle 435$ $\displaystyle 502$
$\displaystyle 613$ $\displaystyle 589$
$\displaystyle 589$ $\displaystyle 591$
$\displaystyle 700$ $\displaystyle 699$
Задание 5:
Таня старше Ани в $\displaystyle 2$ раза, а Ваня на $\displaystyle 7$ лет старше Ани. Сколько лет Ване, если Тане $\displaystyle 16$ лет?
Ответ: лет.
Задание 6:
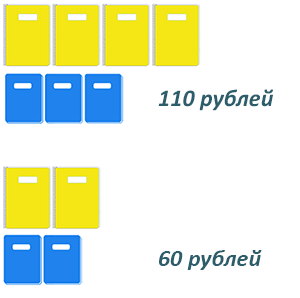
$\displaystyle 4$ блокнота и $\displaystyle 3$ тетради стоят $\displaystyle 110$ рублей, а $\displaystyle 2$ блокнота и $\displaystyle 2$ тетради — $\displaystyle 60$ рублей. Сколько стоят два блокнота?
Ответ: рублей.
Задание 7:

В бидон помещается $\displaystyle 15$ л молока, а в банку — в $\displaystyle 5$ раз меньше. Сколько нужно банок, чтобы разлить в них молоко из шести полных бидонов?
Ответ: банок.
Задание 8:
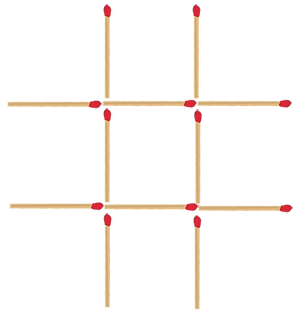
Из $\displaystyle 12$ спичек составлена фигура. Можно ли убрать $\displaystyle 2$ спички и переложить $\displaystyle 2$ спички так, чтобы получилось $\displaystyle 3$ одинаковых квадрата?
Задание 9:
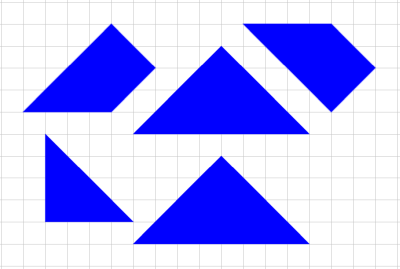
Начерти и вырежи такие фигуры. Можно ли из этих пяти фигур сложить квадрат?
Задание 10:
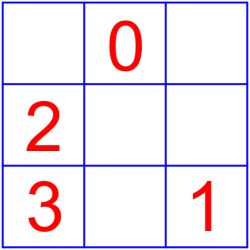
Расставь в свободные клетки квадрата числа $\displaystyle 4, \ 5, \ 6, \ 7, \ 8$ так, чтобы суммы чисел во всех строках, столбцах и на двух диагоналях были бы равными. Какое число будет записано в верхней строке справа?
Ответ:
20 урок
Объёмные фигуры
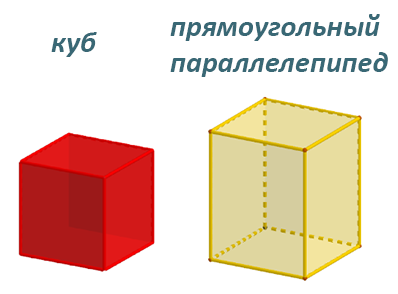
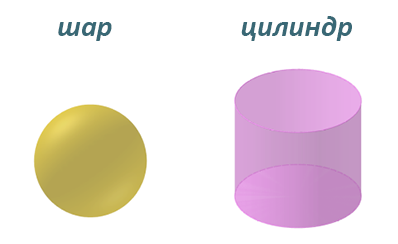
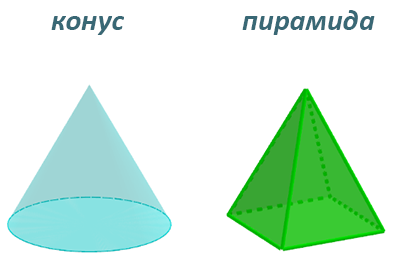
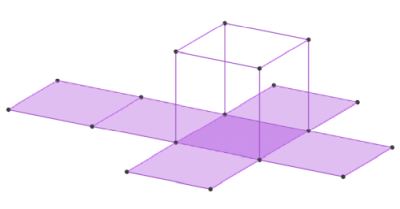
Развёртка куба
Задание 1:
Запиши числа цифрами:
пятьсот тысяч десять
Ответ:
двадцать тысяч сто пятьдесят
Ответ:
три миллиона тридцать
Ответ:
девять миллионов двести девять
Ответ:
тридцать миллионов пять тысяч триста
Ответ:
Задание 2:
Вычисли:
$\displaystyle 900-(240+180):60·105=$
$\displaystyle 800+(320:40-360:90)·13=$
$\displaystyle (700-270:30)·(44:22+33·0)=$
$\displaystyle (600+45:45):(55:55+60·10)=$
$\displaystyle 500-(32+50:25)-(48-24·2)=$
Задание 3:
Реши уравнение:
$\displaystyle x·40=160:2$
Ответ: $\displaystyle x=$
$\displaystyle x·22=90+20$
Ответ: $\displaystyle x=$
$\displaystyle x:12=15·4$
Ответ: $\displaystyle x=$
$\displaystyle 600:x=500:50$
Ответ: $\displaystyle x=$
$\displaystyle x+x=1000-800$
Ответ: $\displaystyle x=$
Задание 4:
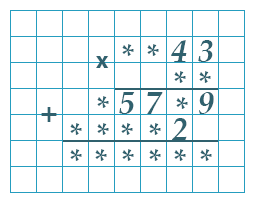
Вставь пропущенные цифры. Назови значение произведения.
Ответ:
Задание 5:
Два велосипедиста отправились из одного посёлка одновременно в противоположных направлениях. Через $\displaystyle 3$ часа расстояние между ними было $\displaystyle 81$ км. Скорость одного из них $\displaystyle 15$ км/ч. Найди скорость другого велосипедиста.
Ответ: км/ч.
Задание 6:
Одна бригада рабочий может отремонтировать $\displaystyle 24$ км дороги за $\displaystyle 30$ дней, а другая — за $\displaystyle 60$ дней. За сколько дней смогут отремонтировать эту дорогу обе бригады, работая вместе?
Ответ: дней.
Задание 7:
Оля в $\displaystyle 5$ раз моложе Коли, а вместе им $\displaystyle 30$ лет. Сколько лет Коле?
Ответ: лет.
Задание 8:
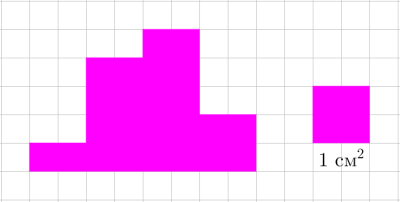
Найди площадь десятиугольника.
Ответ: см$\displaystyle ^2$.
Задание 9:
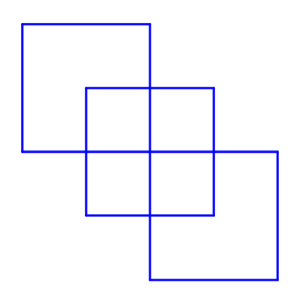
Сколько квадратов на картинке?
Ответ:
Задание 10:
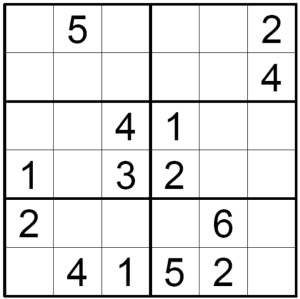
Заполни свободные клетки цифрами от $\displaystyle 1$ до $\displaystyle 6$ так, чтобы в каждой строке, в каждом столбце и в выделенном прямоугольнике $\displaystyle 2$ на $\displaystyle 3$ каждая цифра встречалась бы только один раз. Какая цифра будет в нижней строке слева?
Ответ:
![[Математический кружок]](/img/logo/header-ru-transparent-v5.png)