![Интернет-кружок по математике, 8 класс, примеры [Интернет-кружок по математике, 8 класс, примеры]](/img/theme/subjects/math-64.png) | Интернет-кружок по математике, 8 класс, примерыИнтернет-кружок по математике, 8 класс, примеры |
Примерные серии задач интернет-кружка
Примерные серии задач интернет-кружка
1 серия (сентябрь) учебного года 2025-2026
Теория:
Модуль числа
Модулем (абсолютной величиной) действительного числа $\displaystyle a$ называется само это число, если оно неотрицательное, и это число, взятое с противоположным знаком, если оно отрицательное.
$\displaystyle \begin{equation*} \lvert a\rvert= \begin{cases} \displaystyle a, \ a\geqslant0\\ \displaystyle -a, \ a<0\end{cases} \end{equation*}$
Геометрический смысл модуля
Модулем (абсолютной величиной) действительного числа $\displaystyle a$ называется расстояние от точки, изображающей число $\displaystyle a$ на числовой прямой, до точки $\displaystyle 0$.
$\displaystyle |3| = 3$
$\displaystyle |0| = 0$
$\displaystyle |-3| = 3$
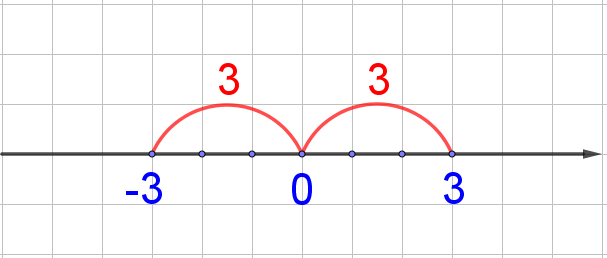
Свойства модуля
$\displaystyle 1)$ $\displaystyle \lvert a\rvert\geqslant0$
$\displaystyle 2)$ $\displaystyle \lvert -a\rvert=\lvert a\rvert$
$\displaystyle 3)$ Если $\displaystyle \lvert a\rvert=b$ при условии $\displaystyle b\geqslant0$, то $\displaystyle a=b$ или $\displaystyle a=-b$.
Решение уравнений с модулем
$\displaystyle 1)$ Решить уравнение: $\displaystyle |2x| = 6$.
Ответ: $\displaystyle 3; -3$.
$\displaystyle 2)$ Решить уравнение: $\displaystyle |- 5x| = - 5$.
Ответ: решений нет.
$\displaystyle 3)$ Решить уравнение: $\displaystyle |8 - 2x| = 0$.
Ответ: $\displaystyle 4$.
Степень с натуральным показателем
Степенью числа $\displaystyle a$ с натуральным показателем $\displaystyle n$, большим $\displaystyle 1$, называется произведение $\displaystyle n$ множителей, каждый из которых равен $\displaystyle a$:
$\displaystyle a^n = \underbrace{a \cdot a \cdot a \dotsc a}_{n} $
Степенью числа $\displaystyle a$ с показателем $\displaystyle 1$ называется само число $\displaystyle a$:
$\displaystyle a^1=a $
В выражении $\displaystyle a^n $ число $\displaystyle a$ - повторяющийся множитель, называют основанием степени, число $\displaystyle n$, показывающее, сколько раз повторяется множитель, называют показателем степени.
Например: $\displaystyle 3^4=3\cdot3\cdot3\cdot3=81$; $\displaystyle 3$ - основание степени, $\displaystyle 4$ - показатель степени, $\displaystyle 81$ - значение степени.
Учимся решать задачи:
Задание 1:
Можно ли восстановить пропущенные цифры, чтобы равенство было верным: $\displaystyle 10 \cdot * = 3 \cdot (3 \cdot * + 5)$? Звёздочки могут обозначать одинаковые цифры, а могут и разные. Число звёздочек соответствует числу цифр.
Варианты ответов:
Задание 2:
Расшифруйте запись, одинаковые буквы - это одинаковые цифры, разные буквы - разные цифры: $\displaystyle TATAT \cdot TO = TOTOTO$. Сколько различных решений имеет эта задача?
Задание 3:
Решите уравнение:
$\displaystyle 1 \cdot 2 \cdot 3 - |9 - 3x| = 1+2+3$.
Задание 4:
Сумма двух многочленов равна $\displaystyle x^3 + x^2 + x +1$. А их разность равна $\displaystyle x^3 - x^2 + x -1$. Назовите эти многочлены
Варианты ответов:
Задание 5:

Два велосипедиста выехали одновременно навстречу друг другу из пунктов $\displaystyle A$ и $\displaystyle B$ и встретились через час. Прибыв в пункты $\displaystyle B$ и $\displaystyle A$ соответственно, велосипедисты сразу же повернули назад и встретились вновь. Через какое время после первой встречи это произошло? Дайте ответ в часах.
Задание 6:
Сколько решений в натуральных числах имеет уравнение: $\displaystyle 2x + 3y + 4z = 9$.
Задание 7:

Решите задачу: сколько автомашин грузоподъёмностью $\displaystyle 3$ т и $\displaystyle 5$ т необходимо для перевозки $\displaystyle 40$ т груза? Можно использовать машины только одного вида, а можно и двух видов - $\displaystyle 3$ т и $\displaystyle 5$ т.
Ответьте на вопрос: сколько решений имеет задача?
Задание 8:
Можно ли из чисел $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$ составить магический квадрат - разместить их в таблице $\displaystyle 3$ на $\displaystyle 3$ так, чтобы суммы чисел по строкам, столбцам и двум диагоналям были одинаковы и так, чтобы число $\displaystyle 7$ было в угловой клетке?
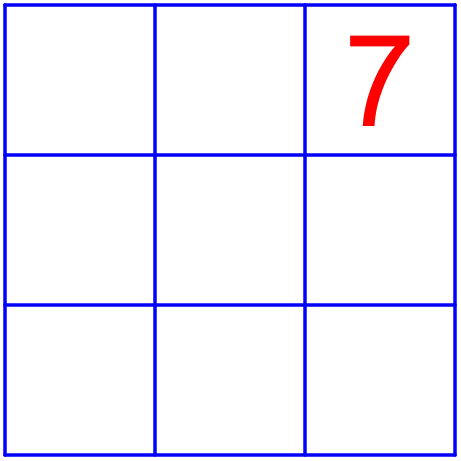
Варианты ответов:
Задание 9:
Можно ли разрезать фигуру по линиям на пять равных, совпадающих при наложении, частей, если разрезанные фигуры можно переворачивать?
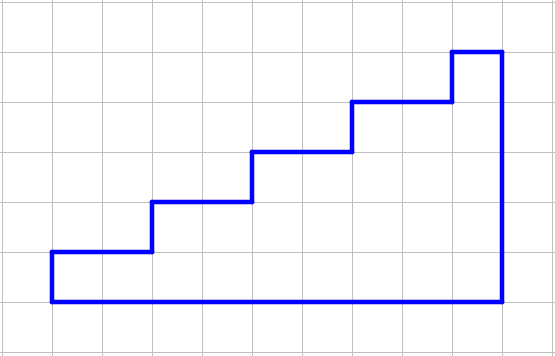
Варианты ответов:
Задание 10:
На двух параллельных прямых отметили семь точек: три на одной и четыре на другой. Сколько существует треугольников с вершинами в этих точках?
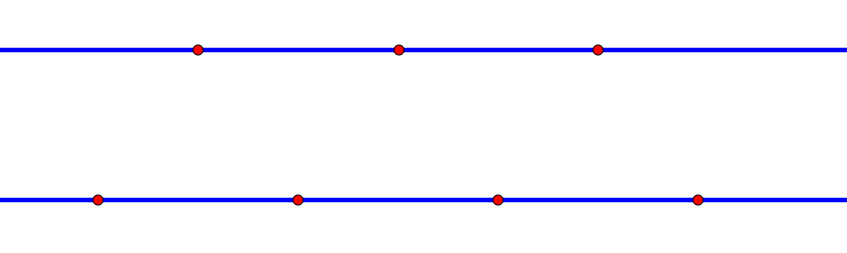
38 серия (май) учебного года 2025-2026
Теория:
Формулы Крамера
Рассмотрим систему линейных уравнений с двумя переменными:
$\displaystyle \begin{cases} \displaystyle a_1x+b_1y=c_1,\\ \displaystyle a_2x+b_2y=c_2. \end{cases}$
Числа $\displaystyle \Delta, \ \Delta_x, \ \Delta_y$ - определители системы.
$\displaystyle \Delta=\begin{vmatrix} a_1 & b_1\\ a_2 & b_2 \end{vmatrix}=a_1b_2-a_2b_1$.
$\displaystyle \Delta_x=\begin{vmatrix} c_1 & b_1\\ c_2 & b_2 \end{vmatrix}=c_1b_2-c_2b_1$.
$\displaystyle \Delta_y=\begin{vmatrix} a_1 & c_1\\ a_2 & c_2 \end{vmatrix}=a_1c_2-a_2c_1$.
При $\displaystyle \Delta \neq 0$ система имеет единственное решение:
$\displaystyle x=\frac{\Delta_x}{\Delta}; \ y=\frac{\Delta_y}{\Delta}$.
При $\displaystyle \Delta=0$:
если $\displaystyle \Delta_x \neq0, \ \Delta_y \neq0$, то система не имеет решений,
если $\displaystyle \Delta_x=0$ или $\displaystyle \Delta_y=0$, то система имеет бесконечное множество решений.
Задача $\displaystyle 1$
Сколько решений имеет система уравнений?
$\displaystyle \begin{cases} \displaystyle 3x+y=8,\\ \displaystyle 4x-5y=2. \end{cases}$
Решение:
$\displaystyle \Delta=\begin{vmatrix} 3 & 1\\ 4 & -5 \end{vmatrix}=3 \cdot (-5) - 4 \cdot 1 = $ $\displaystyle -19$
При $\displaystyle \Delta \neq 0$ система имеет единственное решение.
Ответ: система имеет единственное решение.
Задача $\displaystyle 2$
Решить систему уравнений:
$\displaystyle \begin{cases} \displaystyle 3x-y=4;\\ \displaystyle 6x-2y=9. \end{cases}$
Решение:
$\displaystyle \Delta = 3 \cdot (-2) - 6 \cdot (-1) = 0$
$\displaystyle \Delta_x = 4\cdot (-2) - 9\cdot (-1) = 1$
$\displaystyle \Delta_y = 3 \cdot 9 - 6 \cdot 4 = 3$
Уравнения системы противоречат друг другу.
Ответ: система не имеет решений.
Задача $\displaystyle 3$
Решить систему уравнений:
$\displaystyle \begin{cases} \displaystyle 2x-3y=4;\\ \displaystyle 6x-9y=12. \end{cases}$
Решение:
$\displaystyle \Delta = 2 \cdot (-9) - 6 \cdot (-3) = 0$
$\displaystyle \Delta_x = 4\cdot (-9) - 12 \cdot (-3) = 0$
$\displaystyle \Delta_y = 2 \cdot 12 - 6 \cdot 4=0$
Ответ: система имеет бесконечное множество решений.
Учимся решать задачи:
Задание 1:
Задание 2:

Ваня расставляет солдатиков по $\displaystyle 10$ в шеренгу. В последней шеренге не хватило трёх солдатиков. Он стал ставить в шеренгу по $\displaystyle 12$ солдатиков - $\displaystyle 7$ осталось. Затем он уложил их в коробки по $\displaystyle 100$ штук - третья коробка оказалась неполной. Сколько всего солдатиков у Вани?
Задание 3:
Варианты ответов:
Задание 4:
Сколько решений имеет система уравнений:
$\displaystyle \begin{cases} \displaystyle 5y=4(x-2),\\ \displaystyle 8x=2(5y+8). \end{cases}$
Варианты ответов:
Задание 5:
Решите уравнение:
$\displaystyle x^4+2x^{3}-11x^{2}-12x+36=0$.
Найдите сумму наибольшего и наименьшего корней уравнения.
Варианты ответов:
Задание 6:
Задание 7:
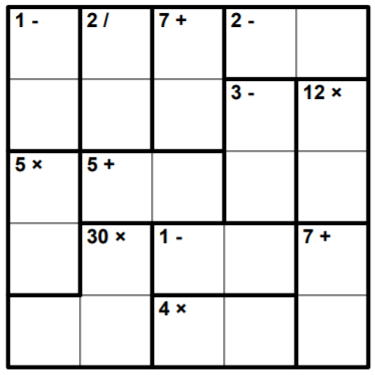
Разгадайте кендоку: заполните клетки числами от $\displaystyle 1$ до $\displaystyle 5$ включительно так, чтобы в каждой строке и в каждом столбце числа не повторялись. Число, которое записано в углу каждого выделенного блока - это результат сложения, вычитания, умножения или деления в этом блоке. Числа внутри блока могут повторяться.
Какое число будет записано в верхней строке в угловой клетке справа?
Задание 8:
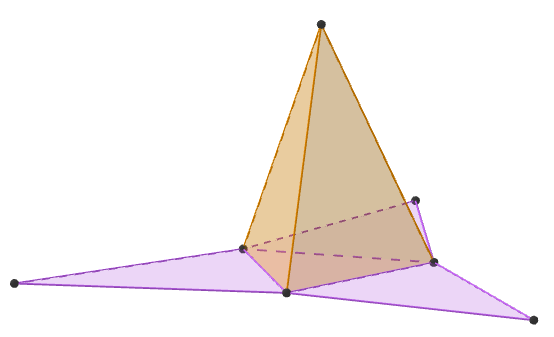
Найдите площадь полной поверхности правильной треугольной пирамиды с ребром $\displaystyle 5$ см.
Варианты ответов:
Задание 9:
Назовите функцию по графику:
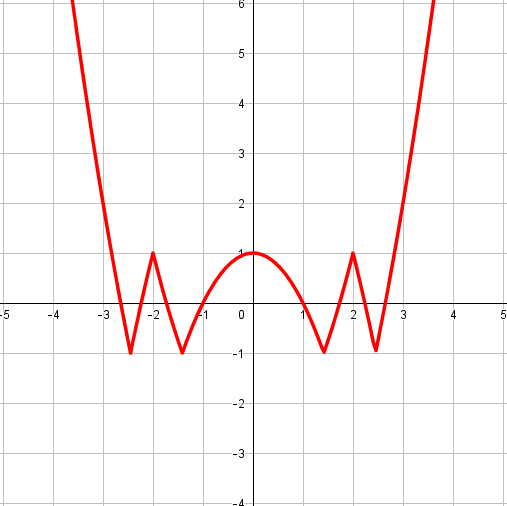
Варианты ответов:
Задание 10:
Какое наибольшее число слонов можно поставить на шахматной доске так, чтобы они не били друг друга?
Ход шахматного слона:

Как записаться в кружок?
- Зарегистрироваться в МетаШколе
- Войти в МетаШколу со своим логином и паролем
- Перейти по ссылке "Все кружки"
- Добавить кружок в корзину.
- Перейти на страницу "Корзина", выбрать способ оплаты, оплатить.
![[Математический кружок]](/img/logo/header-ru-transparent-v5.png)