![Интернет-кружок по математике, 7 класс, примеры [Интернет-кружок по математике, 7 класс, примеры]](/img/theme/subjects/math-64.png) | Интернет-кружок по математике, 7 класс, примерыИнтернет-кружок по математике, 7 класс, примеры |
Примерные серии задач интернет-кружка
Примерные серии задач интернет-кружка
1 серия (сентябрь) учебного года 2025-2026
Теория:
Уравнения
Уравнение - это равенство, содержащее неизвестное число, обозначенное буквой.
Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа от знака равенства - правой частью уравнения.
Каждое слагаемое левой и правой части уравнения называется членом уравнения.
Корнем уравнения называется то значение неизвестного, при котором это уравнение обращается в верное равенство.
Решить уравнение - это значит найти все его корни или установить, что их нет.
Основные свойства уравнений
$\displaystyle 1$) Любой член уравнения можно перенести из одной части в другую, изменив его знак на противоположный.
$\displaystyle 2$) Обе части уравнения можно умножить или разделить на одно и то же число, не равное нулю.
Равносильные уравнения
Уравнения, имеющие одно и то же множество корней, называются равносильными.
Уравнения, не имеющие корней, также считаются равносильными.
Модуль числа
Модулем (абсолютной величиной) действительного числа $\displaystyle a$ называется само это число, если оно неотрицательное, и это число, взятое с противоположным знаком, если оно отрицательное.
$\displaystyle \begin{equation*} \lvert a\rvert= \begin{cases} \displaystyle a,& \ a\geqslant0\\ \displaystyle -a,& \ a<0\end{cases} \end{equation*}$
Геометрический смысл модуля
Модулем (абсолютной величиной) действительного числа $\displaystyle a$ называется расстояние от точки, изображающей число $\displaystyle a$ на числовой прямой, до точки $\displaystyle 0$.
$\displaystyle |3| = 3$
$\displaystyle |0| = 0$
$\displaystyle |-3| = 3$

Решение уравнений с модулем
$\displaystyle 1)$ Решить уравнение: $\displaystyle |x| = 7$.
Ответ: $\displaystyle 7;\ -7$.
$\displaystyle 2)$ Решить уравнение: $\displaystyle |x| = -5$.
Ответ: решений нет.
$\displaystyle 3)$ Решить уравнение: $\displaystyle |x - 1| = 0$.
Ответ: $\displaystyle 1$.
Десятичная система счисления
Натуральные числа - для счёта предметов.
Это числа $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ \dots$
Ряд натуральных чисел бесконечен.
Цифры: $\displaystyle 0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.
Число $\displaystyle 10$ – основание системы счисления.
Счёт идёт десятками, сотнями, тысячами и так далее.
Единица каждого следующего разряда в $\displaystyle 10$ раз больше единицы предыдущего разряда.
Разложение по разрядам:
$\displaystyle 3456 = $ $\displaystyle 3 \cdot 10 \cdot 10 \cdot 10 + 4 \cdot 10 \cdot 10\ + $ $\displaystyle 5 \cdot 10\ + $ $\displaystyle 6 = $ $\displaystyle 3 \cdot 1000 + 4 \cdot 100 + 5 \cdot 10 + 6$.
Признаки делимости:
на $\displaystyle 2$ - натуральное число оканчивается чётной цифрой $\displaystyle 0,\ 2,\ 4,\ 6,\ 8$;
на $\displaystyle 5$ - натуральное число оканчивается цифрой $\displaystyle 0$ или $\displaystyle 5$;
на $\displaystyle 10$ - натуральное число оканчивается цифрой $\displaystyle 0$;
на $\displaystyle 9$ - сумма цифр числа делится на $\displaystyle 9$;
на $\displaystyle 3$ - сумма цифр числа делится на $\displaystyle 3$;
на $\displaystyle 4$ - две последние цифры числа образуют двузначное число, делящееся на $\displaystyle 4$; например, число $\displaystyle 7924$ делится на $\displaystyle 4$, так как число $\displaystyle 24$ делится на $\displaystyle 4$;
на $\displaystyle 8$ - три последние цифры числа образуют трёхзначное число, делящееся на $\displaystyle 8$; например, число $\displaystyle 79168$ делится на $\displaystyle 8$, так как число $\displaystyle 168$ делится на $\displaystyle 8$.
Учимся решать задачи:
Задание 1:
Даны последовательные числа: $\displaystyle -3,\ -2,\ -1,\ 0,\ 1,\ 2,\ 3$. Сколько троек последовательных чисел можно составить из этих чисел, сумма которых равна их произведению?
Задание 2:
Какое двузначное число в $\displaystyle 19$ раз больше цифры его единиц?
Задание 3:
Первое число составляет $\displaystyle 80\%$ второго, второе – $\displaystyle 40\%$ третьего, а третье – $\displaystyle 20\%$ четвёртого. Найдите первое число, если сумма всех четырёх чисел равна $\displaystyle 336$.
Задание 4:
Сколько решений имеет уравнение:
$\displaystyle 1{,}5:0{,}05+|3x|=1{,}5 \cdot 40$?
Задание 5:
Пятнадцать лет назад Настя была в $\displaystyle 5$ раз старше своей сестры Тани. А через $\displaystyle 20$ лет Настя будет в $\displaystyle 1{,}5$ раза старше Тани. Сколько сейчас лет Насте? Дайте ответ в годах.
Задание 6:

Три велосипедиста одновременно стартовали по круговой дорожке. Первый делает полный круг за $\displaystyle 21$ мин, второй – за $\displaystyle 35$ мин, а третий – за $\displaystyle 15$ мин. Через сколько минут они ещё раз окажутся вместе на старте? Дайте ответ в минутах.
Задание 7:

Расшифруйте ребус, одинаковые буквы - это одинаковые цифры, разные буквы - разные цифры: $\displaystyle БАРБОС + БОБИК = СОБАКИ$. Известно, что $\displaystyle Б = 7$. Сколько решений имеет задача?
Задание 8:
Можно ли из чисел $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$ составить магический квадрат - разместить их в таблице $\displaystyle 3$ на $\displaystyle 3$ так, чтобы суммы чисел по строкам, столбцам и двум диагоналям были одинаковы и так, чтобы число $\displaystyle 3$ было в угловой клетке?

Варианты ответов:
Задание 9:
Можно ли разрезать фигуру по линиям на четыре равные, совпадающие при наложении, части, если разрезанные фигуры можно поворачивать и переворачивать?

Варианты ответов:
Задание 10:
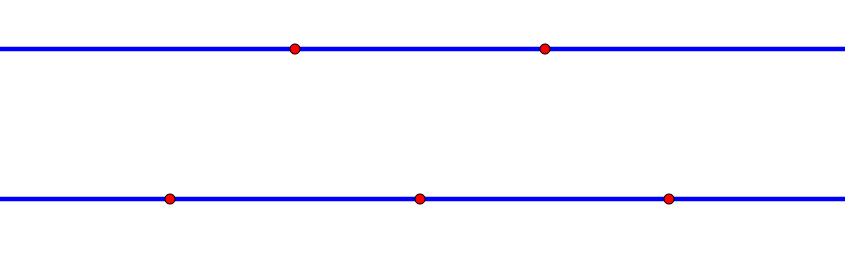
На двух параллельных прямых отметили пять точек: две на одной и три на другой. Сколько существует треугольников с вершинами в этих точках?
38 серия (май) учебного года 2025-2026
Теория:
Формулы Крамера
Рассмотрим систему линейных уравнений с двумя переменными:
$\displaystyle \begin{cases} \displaystyle a_1x+b_1y=c_1,\\ \displaystyle a_2x+b_2y=c_2. \end{cases}$
Числа $\displaystyle \Delta, \ \Delta_x, \ \Delta_y$ - определители системы.
$\displaystyle \Delta=\begin{vmatrix} a_1 & b_1\\ a_2 & b_2 \end{vmatrix}=a_1b_2-a_2b_1$.
$\displaystyle \Delta_x=\begin{vmatrix} c_1 & b_1\\ c_2 & b_2 \end{vmatrix}=c_1b_2-c_2b_1$.
$\displaystyle \Delta_y=\begin{vmatrix} a_1 & c_1\\ a_2 & c_2 \end{vmatrix}=a_1c_2-a_2c_1$.
При $\displaystyle \Delta \neq 0$ система имеет единственное решение:
$\displaystyle x=\frac{\Delta_x}{\Delta}; \ y=\frac{\Delta_y}{\Delta}$.
При $\displaystyle \Delta=0$:
если $\displaystyle \Delta_x \neq0, \ \Delta_y \neq0$, то система не имеет решений,
если $\displaystyle \Delta_x=0$ или $\displaystyle \Delta_y=0$, то система имеет бесконечное множество решений.
Задача $\displaystyle 1$
Сколько решений имеет система уравнений?
$\displaystyle \begin{cases} \displaystyle 2x+y=7,\\ \displaystyle 5x-3y=2. \end{cases}$
Решение:
$\displaystyle \Delta=\begin{vmatrix} 2 & 1\\ 5 & -3 \end{vmatrix}=2 \cdot (-3) - 5 \cdot 1 = $ $\displaystyle -11$
При $\displaystyle \Delta \neq 0$ система имеет единственное решение.
Ответ: система имеет единственное решение.
Задача $\displaystyle 2$
Решить систему уравнений:
$\displaystyle \begin{cases} \displaystyle 4x-y=5;\\ \displaystyle 8x-2y=3. \end{cases}$
Решение:
$\displaystyle \Delta = 4 \cdot (-2) - 8 \cdot (-1) = 0$
$\displaystyle \Delta_x = 5\cdot (-2) - 3\cdot (-1) = -7$
$\displaystyle \Delta_y = 4 \cdot 3 - 8 \cdot 5 = -28$
Уравнения системы противоречат друг другу.
Ответ: система не имеет решений.
Задача $\displaystyle 3$
Решить систему уравнений:
$\displaystyle \begin{cases} \displaystyle x-2y=1;\\ \displaystyle 3x-6y=3. \end{cases}$
Решение:
$\displaystyle \Delta = 1 \cdot (-6) - 3 \cdot (-2) = 0$
$\displaystyle \Delta_x = 1\cdot (-6) - 3 \cdot (-2) = 0$
$\displaystyle \Delta_y = 1 \cdot 3 - 3\cdot 1=0$
Ответ: система имеет бесконечное множество решений.
Учимся решать задачи:
Задание 1:
Задание 2:
Задание 3:
Сколько решений имеет система уравнений:
$\displaystyle \begin{cases} \displaystyle 3x+5y=7,\\ \displaystyle 9x+15y=17. \end{cases}$
Варианты ответов:
Задание 4:
Варианты ответов:
Задание 5:
Варианты ответов:
Задание 6:
$\displaystyle \begin{cases} \displaystyle 2x+y+z=7,\\ \displaystyle x+2y+z=8. \end{cases}$
Известно, что $\displaystyle x,\ y,\ z$ - натуральные числа.
Задание 7:

Пешеход заметил, что через каждые $\displaystyle 12$ мин его обгоняет трамвай, а через каждые $\displaystyle 6$ мин он встречает трамвай. Считая движение равномерным, найдите интервалы между каждыми двумя трамваями. Дайте ответ в минутах.
Задание 8:
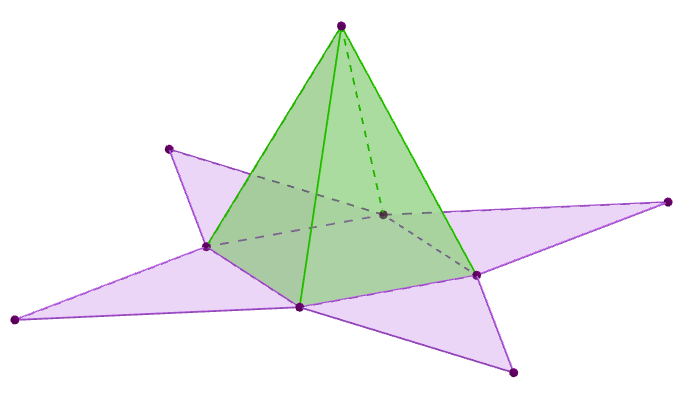
Найдите площадь полной поверхности правильной четырёхугольной пирамиды, если периметр основания равен $\displaystyle 16$ см, а высота боковой грани - $\displaystyle 6$ см.
Варианты ответов:
Задание 9:
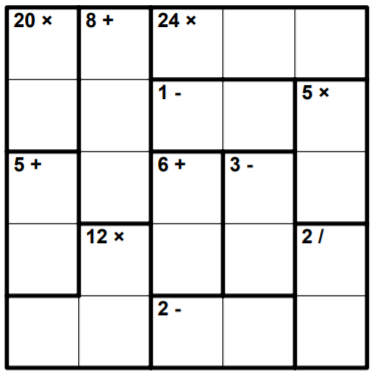
Разгадайте кендоку: заполните клетки числами от $\displaystyle 1$ до $\displaystyle 5$ включительно так, чтобы в каждой строке и в каждом столбце числа не повторялись. Число, которое записано в углу каждого выделенного блока - это результат сложения, вычитания, умножения или деления в этом блоке. Числа внутри блока могут повторяться.
Какое число будет записано в нижней строке в угловой клетке слева?
Задание 10:
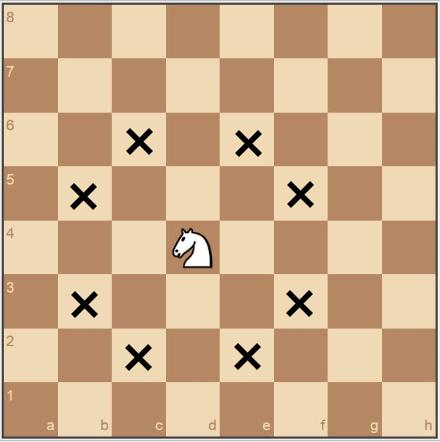
Какое наибольшее число, не бьющих друг друга коней, можно поставить на шахматной доске?
Ход шахматного коня:
Как записаться в кружок?
- Зарегистрироваться в МетаШколе
- Войти в МетаШколу со своим логином и паролем
- Перейти по ссылке "Все кружки"
- Добавить кружок в корзину.
- Перейти на страницу "Корзина", выбрать способ оплаты, оплатить.
![[Математический кружок]](/img/logo/header-ru-transparent-v5.png)