![ЕГЭ по математике (профильный уровень) для 10-11 классов [ЕГЭ по математике (профильный уровень) для 10-11 классов]](/img/theme/subjects/math-64.png) | ЕГЭ по математике (профильный уровень) для 10-11 классовЕГЭ по математике (профильный уровень) для 10-11 классов |
Уравнения с одной переменной
Число называется корнем уравнения, если при подстановке этого числа в неизвестное уравнение обращается в верное числовое равенство.
Решить уравнение означает найти множество всех его корней или доказать, что их нет.
При решении уравнений допустимы следующие равносильные преобразования:
1. Перенос слагаемого из одной части уравнения в другую с противоположным знаком.
2. Умножение (или деление) обеих частей уравнения на ненулевое число.
3. Равносильное преобразование одной из частей уравнения, не изменяющее область допустимых значений переменной.
При решении уравнений некоторых видов возможно использование определённого алгоритма, например, при решении квадратного уравнения можно найти дискриминант квадратного уравнения, и если он неотрицательный, то по формуле корней квадратного уравнения можно далее найти его корни.
Иррациональное уравнение вида $\displaystyle \sqrt {f(x)} = g(x)$ может быть решено по следующему алгоритму: $\displaystyle f(x) = {g(x)}^2 $ при условии $\displaystyle g(x) \geq 0$.
Другой способ решения такого уравнения состоит в возведении в квадрат обеих частей, что не является равносильным преобразованием и может привести к появлению посторонних корней, поэтому в таком случае требуется проверка каждого из полученных корней подстановкой в исходное уравнение.
При решении уравнений в тестовой части ЕГЭ настоятельно рекомендуем в любом случае осуществлять проверку.
Преобразование выражений
Для преобразования алгебраических выражений полезными будут следующие свойства дроби и степени:
$\displaystyle \frac {a}{b} = \frac {a \cdot c}{b \cdot c}$ и $\displaystyle \frac {a}{b} = \frac {a : c}{b : c}$ при $\displaystyle c \neq0$,
$\displaystyle \frac {a}{b} \cdot \frac {c}{d}=\frac {ac}{bd}, \frac {a}{b} : \frac {c}{d}=\frac {ad}{bc}, \frac {a}{b} + \frac {c}{d}=\frac {ad+bc}{bd}, \frac {a}{m} + \frac {b}{m}=\frac {a+b}{m}$.
$\displaystyle a^0=1, a^1=1, a^{-n}=\frac {1}{a^n}, a ^ {1/n} =\sqrt [n] {a}, a ^ {m/n} =\sqrt [n] {a^m},$
$\displaystyle a^m \cdot a^n = a^ {m+n}, a^m : a^n = a^ {m-n}, (a^m)^n= a^{mn}, a^n \cdot b^n = (ab)^n, a^n : b^n = (\frac {a}{b})^n$.
Нахождение наибольшего/наименьшего значения функции без взятия производной
Квадратичная функция $\displaystyle y= a x^2+bx+c$, где $\displaystyle a \neq 0$,
при $\displaystyle a>0$ достигает своего наибольшего значения при $\displaystyle x_0 = - \frac {b}{2a}$ и не достигает своего наименьшего значения,
при $\displaystyle a<0$ достигает своего наименьшего значения при $\displaystyle x_0 = - \frac {b}{2a}$ и не достигает своего наибольшего значения.
Также наибольшее или наименьшее значение квадратичной функции можно находить с помощью выделения полного квадрата.
Аналогично можно найти наибольшее или наименьшее значение функции вида $\displaystyle y= \sqrt {a x^2+bx+c}$, где $\displaystyle a \neq 0$, при условии, что область определения этой функции отлична от пустого множества.
Задание 1:
Теплоход рассчитан на 846 пассажиров и 24 членов команды. Каждая спасательная шлюпка может вместить 65 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды? Ответ:
Задание 2:
Диагональ экрана телевизора равна 64 дюймам. Выразите диагональ экрана в сантиметрах. Считайте, что 1 дюйм равен 2,54 см. Результат округлите до целого числа. Ответ:
Задание 3:
На рисунке жирными точками показано суточное количество осадков, выпадавших в некотором городе с 3 по 15 марта 1960 года. По горизонтали указаны числа месяца, по вертикали —количество осадков, выпавших в соответствующий день, в миллиметрах. Для наглядности жирные точки на рисунке соединены линией. Определите по рисунку наибольшее суточное количество осадков, выпадавших в этом городе в период с 3 по 10 марта. Ответ дайте в миллиметрах. Ответ:
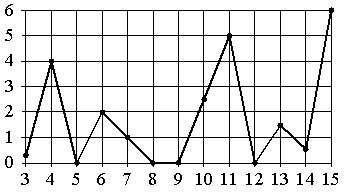
Задание 4:
При работе фонарика батарейка постепенно разряжается и напряжение в электрической цепи фонарика падает. На графике показана зависимость напряжения в цепи от времени работы фонарика. На горизонтальной оси отмечено время работы фонарика в часах, на вертикальной оси - напряжение в вольтах. Определите по рисунку, на сколько вольт упало напряжение за первые 15 часов работы. Ответ:

Задание 5:
Решите уравнение $\displaystyle (5x+7)^2=(5x-9)^2$. Если уравнение имеет более одного корня, то в ответе укажите меньший из них. Ответ:
Задание 6:
Решите уравнение $\displaystyle \sqrt{4-3x}=x$. Если уравнение имеет более одного корня, то в ответе укажите меньший из них. Ответ:
Задание 7:
Вычислите значение выражения: $\displaystyle \frac {\sqrt[9]{5} \cdot \sqrt[18]{5}} {\sqrt[3]{125} \cdot \sqrt[12] {25}} $
Ответ:
Задание 8:
Вычислите значение выражения: $\displaystyle \frac {5^{1{,}9} \cdot 6^{4{,}9}} {30^{2{,}9}} $
Ответ:
Задание 9:
Найдите наименьшее значение функции $\displaystyle y= \sqrt {x^2 -28x+197}$. Ответ:
Задание 10:
Найдите наибольшее значение функции $\displaystyle y= \sqrt {-x^2+18x-72}$. Ответ:
Основные понятия
Будем рассматривать некоторый опыт (эксперимент), результатом которого может быть один из конечного числа исходов.
Событие – то, что наблюдаем в результате опыта. Возможно при нескольких (благоприятных) исходах.
Достоверным называется событие, для которого все исходы опыта являются благоприятными.
Невозможным называется событие, для которого ни один исход опыта не является благоприятным.
Случайным называется событие, для которого среди исходов есть и благоприятные, и неблагоприятные.
Вероятность в математике – число в границах от 0 до 1 (при заполнении бланка тестовой части ЕГЭ - это только конечная десятичная дробь).
Запись: 0,6 - верный формат; 3/5, 3:5, 60% - неверные форматы
Вероятность события $\displaystyle A $ обозначается как $\displaystyle P(A) $.
Таким образом, в математике $\displaystyle 0 \leq P(A) \leq 1 $. При этом и 0, и 1 достигаются: $\displaystyle P(A)=0 $ для невозможного события и $\displaystyle P(A)=1 $ для достоверного события.
Объединением событий $\displaystyle A_k $ называется событие $\displaystyle A $, которое означает появление хотя бы одного из событий $\displaystyle A_k $.
Обозначение: объединение событий $\displaystyle A $ и $\displaystyle B $: $\displaystyle A\cup B .$ Вероятность объединения событий $\displaystyle P(A\cup B) .$
Пересечением событий $\displaystyle A_k $ называется событие $\displaystyle A $, которое заключается в осуществлении всех событий $\displaystyle A_k $.
Обозначение: пересечение событий $\displaystyle A $ и $\displaystyle B $: $\displaystyle A\cap B $. Вероятность пересечения событий $\displaystyle A $ и $\displaystyle B $: $\displaystyle P(A\cap B).$
События $\displaystyle A $ и $\displaystyle B $ называются несовместными, если появление одного из них исключает появление другого.
Дополнительным (противоположным) к событию$\displaystyle A $ называется событие $\displaystyle \overline {A} $, обозначающее, что событие $\displaystyle A $ не происходит.
Объединение и пересечение событий лучше всего представлять в виде кругов (диаграмм) Эйлера - на плоскости множества схематично изображаются кругами или овалами (или другими фигурами). "Круг", соответствующий событию, означает множество благоприятных ему исходов. Пересечение "кругов", т. е. событий, означает множество исходов, благоприятных для всех пересечённых событий. Несовместные события изображаются непересекающимися "кругами".
Свойства вероятностей
1. Формула включений и исключений для событий (также встречается как теорема сложения вероятностей):
для событий $\displaystyle A $ и $\displaystyle B $ верно: $\displaystyle P(A\cup B)=P(A)+P(B)-P(A\cap B) $
Частный случай для несовместных событий: $\displaystyle P(A\cup B)=P(A)+P(B) $, то есть вероятность объединения (суммы) двух несовместных событий равна сумме вероятности этих событий.
Частный случай для противоположных событий верно: $\displaystyle P(A)+P(\overline {A})=1 $, то есть сумма вероятностей противоположных событий равна 1.
2. Независимость событий
Определение: События $\displaystyle A $ и $\displaystyle B $ называются независимыми, если верно следующее: $\displaystyle P(A∩B)=P(A)⋅P(B) $.
Итак:
Если $\displaystyle P(A∩B)=P(A)⋅P(B) $, то события $\displaystyle A $ и $\displaystyle B $ называются независимыми.
И наоборот: если в условии задачи сказано, что события $\displaystyle A $ и $\displaystyle B $ независимы, то в решении можно использовать $\displaystyle P(A∩B)=P(A)⋅P(B) $.
Известно, что результаты бросков монеты – независимые события (результат 1-го и результат 2-го, или 3-го и т.д.) Результаты бросков игральных костей (результат, выпавший на первой кости, и результат, выпавший на второй кости) – тоже независимы.
Будьте внимательны:
в некоторых случаях верно P(A∩B)=P(A)∙P(B),
а в некоторых случаях P(A∩B)≠P(A)∙P(B).
! Известно, что результаты бросков монеты – независимые события (результат 1-го и результат 2-го, или 3-го и т.д.)
Результаты бросков игральных костей (результат, выпавший на первой кости, и результат, выпавший на второй кости) – тоже независимы.
При этом стоит отметить, что когда речь идет о событиях, где событие A, например, связано с результатом броска одной монеты (кубика), а событие В - с результатом другой монеты (кубика), то данные события будут независимы. (Стоит уточнить, что речь идёт о событиях, каждое из которых связанно с результатом различных бросков монеты или кубика)
Также известно, что если события А и В – независимые, то независимы все пары событий: неА и неВ, неА и В , А и неВ .
При решении задачи использовать P(A∩B)=P(A)⋅P(B) можно с уверенностью только в том случае, если известно, что события A и B независимыми (например, если это сказано в условии).
Произведение вероятностей с уверенностью можно использовать, только если в условии уточнено, что описываемые события независимы. Также это правило можно применять в ситуации, когда проведена серия бросков монеты или игрального кубика, и каждое событие относится к результату отдельного броска.
3. Вероятность появления "хотя бы одного" из событий
Если требуется найти вероятность появления хотя бы одного события:
Удобнее находить вероятность появления хотя бы одного события из $\displaystyle A_1, A_2, ... A_k$ через противоположное событие:
События "Произойдёт хотя бы одно из событий $\displaystyle A_1, A_2, ... A_k$" (это объединение $\displaystyle A_1, A_2, ... A_k$) и "Не произойдет ни одно из событий $\displaystyle A_1, A_2, ... A_k$" (это пересечение не$\displaystyle A_1,$ не$\displaystyle A_2,$ ... не$\displaystyle A_k$) - противоположные (дополнительные), значит
$\displaystyle P(A_1 \cup A_2 \cup ... \cup A_k)=1 - P(\overline {A_1} \cap \overline {A_2} \cap ... \cap \overline {A_k}).$
То есть вероятность того, что произойдёт хотя бы одно из событий $\displaystyle A_1, A _2,... A_k$ равна разности 1 и вероятности того, что одновременно не произойдут $\displaystyle A_1,$ и $\displaystyle A _2,$ и ... и $\displaystyle A_k.$
Если при этом известно, что события $\displaystyle A_1, A_2, ... A_k$ - независимые, то:
$\displaystyle P(A_1 \cup A_2 \cup ... \cup A_k)=1 - P(\overline {A_1}) \cdot P( \overline {A_2} )\cdot ... \cdot P( \overline {A_k}).$ (!только если известно, что события независимы!)
4. Формула полной вероятности, условная вероятность
Определение: События $\displaystyle A_1, A_2, ... A_k$ образуют полную группу событий, если никакие два из них не являются совместными и хотя бы одно из событий точно произойдёт, то есть $\displaystyle P(A_1 \cup A_2 \cup ... \cup A_k)=1.
Определение: Условной вероятностью события $B$\displaystyle при условии события $A$\displaystyle называется вероятность того, что событие $B$\displaystyle произошло при условии, что произошло событие $A$\displaystyle . Обозначение: $P(B|A).$\displaystyle
Формула полной вероятности:
Если дана полная группа событий $A_1, A_2, ... A_k$\displaystyle и известны условные вероятности события $B$\displaystyle при каждом из событий $A_i:$\displaystyle $P(B|A_1),P(B|A_2)...P(B|A_k),$\displaystyle то вероятность события $B$\displaystyle можно вычислить следующим образом:
$P(B)=P(A_1)\cdot P(B|A_1)+P(A_2)\cdot P(B|A_2)+...+P(A_k)\cdot P(B|A_k).$\displaystyle
Нахождение условной вероятности в опыте с конечным числом равновозможных исходов:
Рассмотрим опыт (эксперимент), в результате которого может произойти один из конечного числа равновозможных(!) исходов. При этом событие $A$\displaystyle происходит в $a$\displaystyle исходах, событие $B$\displaystyle происходит в $b$\displaystyle исходах, а одновременно события $A$\displaystyle и $B$\displaystyle (то есть событие $A \cap B$\displaystyle ) происходит в $c$\displaystyle исходах.
Тогда условная вероятность события $B$\displaystyle при условии события $A$\displaystyle равна отношению $c$\displaystyle к $a:$\displaystyle
$P(B|A)= \frac {c}{a}.$\displaystyle
Другими словами, для того, чтобы найти такую условную вероятность, надо "сконцентрироваться" на тех исходах, когда осуществляется событие $A,$\displaystyle вычислить их число, далее только среди этих исходов найти те, при которых осуществляется событие $B, $\displaystyle вычислить их количество, и поделить последнее число на предыдущее.
Задание 1:
По статистике среди новорожденных 51% - мальчики и 49% - девочки. Дальтонизм встречается у 8% мужского населения и у 1% женского. С какой вероятностью новорожденный малыш будет дальтоником? Ответ:
Задание 2:
Михаил Петрович смотрит вечером телевизор, случайно переключая каналы. С вероятностью 0,6 он попадает на сериал, с вероятностью 0,1 – на ток-шоу, а с вероятностью 0,3 – на новости. При этом, если Михаил Петрович смотрит сериал, то вероятность что он уснёт составляет 0,5, если ток-шоу -вероятность уснуть равна 0,3, а если новости – 0,4. С какой вероятностью Михаил Петрович уснёт во время просмотра телевизора? Ответ:
Задание 3:
Две одинаковые лампочки, каждая из которых может бесперебойно работать в течение первого года работы с вероятностью 0,7, могут одновременно бесперебойно работать в течение первого года работы с вероятностью 0,66. С какой вероятностью хотя бы одна лампочка прослужит больше года? Ответ:
Задание 4:
В торговом центре работают два банкомата. Известно, что вероятность события «Первый банкомат будет работать весь день» равна 0,8. Такая же вероятность события «Второй банкомат будет работать весь день». Вероятность того, что оба банкомата проработают без перебоев весь день, равна 0,75. Найдите вероятность того, что к вечеру оба банкомата выйдут из строя. Ответ:
Задание 5:
Вероятность попадания в цель при стрельбе из первого орудия равна 0,85, а при стрельбе из второго 0,8. Были произведены по одному выстрелу из каждого орудия. Результаты выстрелов – независимы. Найдите вероятность попадания в цель сразу из двух орудий. Ответ:
Задание 6:
В партии одинаковых лампочек каждая из них может перегореть в течение первого года службы с вероятностью 0,4. Если выбрать две лампочки, работающие независимо друг от друга, то с какой вероятностью хотя бы одна прослужит больше года? Ответ:
Задание 7:
Стрелок попадает в мишень с вероятностью 0,9. Результаты выстрелов независимы друг от друга. С какой вероятностью стрелок поразит мишень только с третьего раза? Ответ:
Задание 8:
Стрелок попадает в мишень с вероятностью 0,9. Результаты выстрелов независимы друг от друга. С какой вероятностью стрелок поразит только одну мишень в трёх попытках? Ответ:
Задание 9:
Найти условную вероятность того, что при бросании двух костей выпало разное число очков, при условии, что в сумме выпало 8. Ответ:
Задание 10:
Монету бросают 3 раза. С какой вероятностью орёл выпадет хотя бы один раз, при условии, что первый раз выпадет решка? Ответ: