![Интернет-кружок по математике, 1 класс, примеры [Интернет-кружок по математике, 1 класс, примеры]](/img/theme/subjects/math-64.png) | Интернет-кружок по математике, 1 класс, примерыИнтернет-кружок по математике, 1 класс, примеры |
Примерные серии задач интернет-кружка
Примерные серии задач интернет-кружка
1 серия (сентябрь) учебного года 2025-2026
Теория:
Цифры: $\displaystyle 0,\ 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.
Натуральные числа $\displaystyle -$ для счёта предметов.
Это числа: $\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ \dots$
Ряд натуральных чисел бесконечен.
Однозначные натуральные числа:
$\displaystyle 1,\ 2,\ 3,\ 4,\ 5,\ 6,\ 7,\ 8,\ 9$.
Двузначные натуральные числа:
$\displaystyle 10,\ 11,\ 12,\ 13,\ ...,\ 99$.
$\displaystyle 1$ десяток $\displaystyle = 10$ единиц
$\displaystyle 1$ сотня $\displaystyle = 10$ десятков
Объёмные фигуры - куб и шар.


Русский алфавит ($\displaystyle 33$ буквы):
А, Б, В, Г, Д, Е, Ё, Ж, З, И, Й, К, Л, М, Н, О, П, Р, С, Т, У, Ф, Х, Ц, Ч, Ш, Щ, Ъ, Ы, Ь, Э, Ю, Я.
Учимся решать задачи:
Задание 1:
Даны цифры: $\displaystyle 1,\ 2,\ 3,\ 4,\ 5$. Составьте из этих цифр двузначное число так, чтобы оно было наибольшим из всех возможных, и чтобы цифры были разными.
Задание 2:
Даны цифры: $\displaystyle 2;\ 5$. Сколько различных двузначных чисел можно составить из этих цифр, если цифры в записи числа могут повторяться?
Задание 3:
Назовите следующее число в ряду:
$\displaystyle 1,\ 3,\ 5,\ 7,\ 9,\ 11,\ ... $
Задание 4:
Сколько надо сделать распилов, чтобы распилить бревно на $\displaystyle 4$ части?
Задание 5:

Ручка дороже тетради, а карандаш дешевле тетради. Что дороже - карандаш или ручка?
Варианты ответов:
Задание 6:
В шахматном турнире с тремя участниками всего было сыграно $\displaystyle 3$ партии. Каждый сыграл одно и то же число партий. Сколько партий сыграл каждый участник?
Задание 7:
Найдите закономерность и запишите пропущенную букву: $\displaystyle А,\ В,\ Д,\ Ё,\ З,\ \dots,\ Л$.
Варианты ответов:
Задание 8:
Какая фигура пропущена?

Варианты ответов:
Задание 9:
Можно ли разрезать фигуру по линиям на две равные, совпадающие при наложении, части, если разрезанные фигуры можно переворачивать?
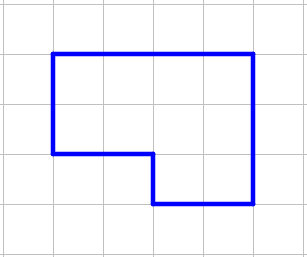
Варианты ответов:
Задание 10:
Сколько кубиков нужно для построения фигуры?

Варианты ответов:
38 серия (май) учебного года 2025-2026
Теория:
Шахматные фигуры
Ход шахматного коня
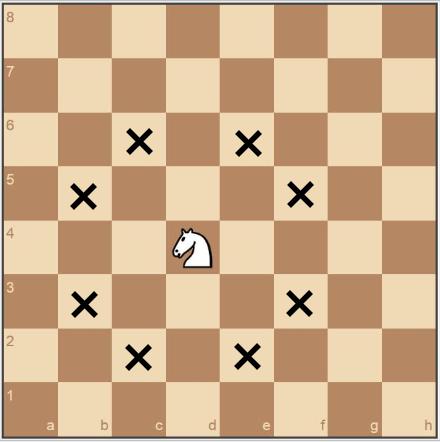
Принцип Дирихле
Задача $\displaystyle 1$
В ящике $\displaystyle 5$ белых шаров, $\displaystyle 7$ чёрных и $\displaystyle 9$ красных. На ощупь шары неотличимы друг от друга. Шары вынимают из ящика в темноте. Какое наименьшее число шаров нужно взять, чтобы среди них обязательно оказалось $\displaystyle 3$ красных шара?
Решение:
В наихудшем случае сначала будут взяты все белые и чёрные, а затем $\displaystyle 3$ красных.
$\displaystyle 5 + 7 + 3 = 15$ шаров.
Ответ: $\displaystyle 15$.
Задача $\displaystyle 2$
В ящике $\displaystyle 5$ белых шаров, $\displaystyle 7$ чёрных и $\displaystyle 9$ красных. На ощупь шары неотличимы друг от друга. Шары вынимают из ящика в темноте. Какое наименьшее число шаров нужно взять, чтобы среди них обязательно оказалось $\displaystyle 2$ шара разного цвета?
Решение:
В наихудшем случае сначала будут взяты $\displaystyle 9$ шаров красного цвета (красных больше всего), а затем достаточно взять $\displaystyle 1$ шар (белый или чёрный), и получится $\displaystyle 2$ шара разного цвета.
$\displaystyle 9+1 = 10$ шаров.
Ответ: $\displaystyle 10$.
Задача $\displaystyle 3$
В ящике $\displaystyle 5$ белых шаров, $\displaystyle 7$ чёрных и $\displaystyle 9$ красных. На ощупь шары неотличимы друг от друга. Шары вынимают из ящика в темноте. Какое наименьшее число шаров нужно взять, чтобы среди них обязательно оказалось $\displaystyle 3$ шара одного цвета?
Решение:
В наихудшем случае сначала будут взяты шары разных цветов по два: два белых, два чёрных и два красных. Если взять ещё один шар, то будет $\displaystyle 3$ шара одного цвета или белого, или чёрного, или красного.
$\displaystyle 2 + 2 + 2 + 1 = 7$ шаров.
Ответ: $\displaystyle 7$.
Учимся решать задачи:
Задание 1:
Задание 2:
Найдите сумму всех чётных натуральных чисел от $\displaystyle 2$ до $\displaystyle 18$ включительно:
$\displaystyle 2 + 4 + 6 + 8 + \dots + 18$.
Задание 3:
Варианты ответов:
Задание 4:
Задание 5:

В коробке $\displaystyle 10$ красных и $\displaystyle 15$ синих шаров. На ощупь шары неотличимы друг от друга. Шары вынимают из ящика в темноте. Какое наименьшее число шаров надо взять, чтобы среди них обязательно оказалось $\displaystyle 5$ красных?
Задание 6:
Задание 7:
Задание 8:
Сколько треугольников можно найти на картинке?
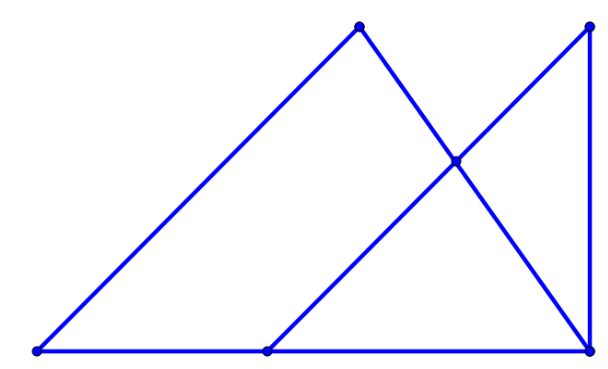
Задание 9:
Сколько прямолинейных разломов надо сделать, чтобы разделить шоколадку на $\displaystyle 6$ отдельных кусочков?

Задание 10:
Можно ли прямоугольник $\displaystyle 3$ на $\displaystyle 4$ обойти шахматным конём, побывав в каждой клеточке один раз?

Варианты ответов:
Как записаться в кружок?
- Зарегистрироваться в МетаШколе
- Войти в МетаШколу со своим логином и паролем
- Перейти по ссылке "Все кружки"
- Добавить кружок в корзину.
- Перейти на страницу "Корзина", выбрать способ оплаты, оплатить.
![[Математический кружок]](/img/logo/header-ru-transparent-v5.png)